Package dynamics (Maxima 5.47post Manual)

56 Package dynamics

The dynamics package
Graphical analysis of discrete dynamical systems
Visualization with VTK

56.1 The dynamics package

Package dynamics includes functions for 3D visualization, animations, graphical analysis of differential and difference equations and numerical solution of differential equations. The functions for differential equations are described in the section on Numerical Methods and the functions to plot the Mandelbrot and Julia sets are described in the section on Plotting.

All the functions in this package will be loaded automatically the first time they are used.

Categories: Dynamical systems · Share packages · Package dynamics ·

56.2 Graphical analysis of discrete dynamical systems

Function: chaosgame ([[x1, y1]…[xm, ym]], [x0, y0], b, n, options, …); ¶

Implements the so-called chaos game: the initial point (x0, y0) is plotted and then one of the m points [x1, y1]…xm, ym] will be selected at random. The next point plotted will be on the segment from the previous point plotted to the point chosen randomly, at a distance from the random point which will be b times that segment’s length. The procedure is repeated n times. The options are the same as for plot2d.

Example. A plot of Sierpinsky’s triangle:

(%i1) chaosgame([[0, 0], [1, 0], [0.5, sqrt(3)/2]], [0.1, 0.1], 1/2,
                 30000, [style, dots]);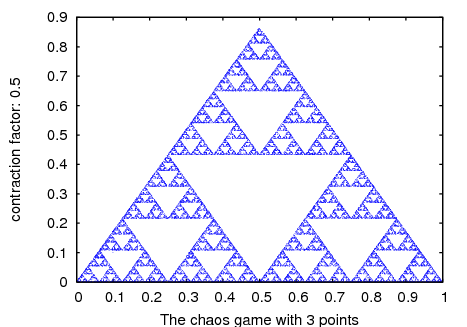

Categories: Package dynamics · Plotting ·

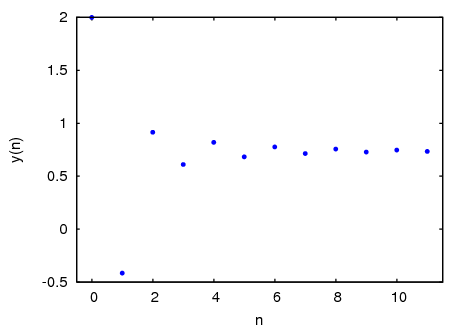
Function: evolution (F, y0, n, …, options, …); ¶

Draws n+1 points in a two-dimensional graph, where the horizontal coordinates of the points are the integers 0, 1, 2, ..., n, and the vertical coordinates are the corresponding values y(n) of the sequence defined by the recurrence relation

        y(n+1) = F(y(n))

With initial value y(0) equal to y0. F must be an expression that depends only on one variable (in the example, it depend on y, but any other variable can be used), y0 must be a real number and n must be a positive integer. This function accepts the same options as plot2d.

Example.

(%i1) evolution(cos(y), 2, 11);

Categories: Package dynamics · Plotting ·

Function: evolution2d ([F, G], [u, v], [u0, y0], n, options, …); ¶

Shows, in a two-dimensional plot, the first n+1 points in the sequence of points defined by the two-dimensional discrete dynamical system with recurrence relations

        u(n+1) = F(u(n), v(n))    v(n+1) = G(u(n), v(n))

With initial values u0 and v0. F and G must be two expressions that depend only on two variables, u and v, which must be named explicitly in a list. The options are the same as for plot2d.

Example. Evolution of a two-dimensional discrete dynamical system:

(%i1) f: 0.6*x*(1+2*x)+0.8*y*(x-1)-y^2-0.9$
(%i2) g: 0.1*x*(1-6*x+4*y)+0.1*y*(1+9*y)-0.4$
(%i3) evolution2d([f,g], [x,y], [-0.5,0], 50000, [style,dots]);

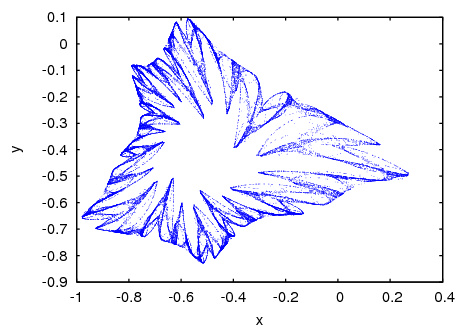
And an enlargement of a small region in that fractal:

(%i9) evolution2d([f,g], [x,y], [-0.5,0], 300000, [x,-0.8,-0.6],
                  [y,-0.4,-0.2], [style, dots]);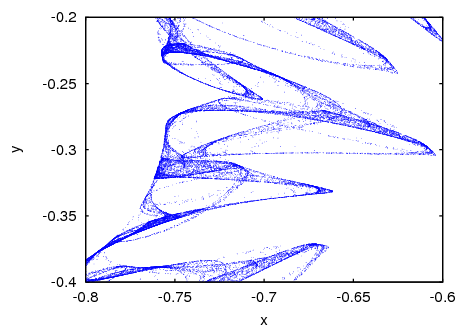

Categories: Package dynamics · Plotting ·

Function: ifs ([r1, …, rm], [A1,…, Am], [[x1, y1], …, [xm, ym]], [x0, y0], n, options, …); ¶

Implements the Iterated Function System method. This method is similar to the method described in the function chaosgame. but instead of shrinking the segment from the current point to the randomly chosen point, the 2 components of that segment will be multiplied by the 2 by 2 matrix Ai that corresponds to the point chosen randomly.

The random choice of one of the m attractive points can be made with a non-uniform probability distribution defined by the weights r1,...,rm. Those weights are given in cumulative form; for instance if there are 3 points with probabilities 0.2, 0.5 and 0.3, the weights r1, r2 and r3 could be 2, 7 and 10. The options are the same as for plot2d.

Example. Barnsley’s fern, obtained with 4 matrices and 4 points:

(%i1) a1: matrix([0.85,0.04],[-0.04,0.85])$
(%i2) a2: matrix([0.2,-0.26],[0.23,0.22])$
(%i3) a3: matrix([-0.15,0.28],[0.26,0.24])$
(%i4) a4: matrix([0,0],[0,0.16])$
(%i5) p1: [0,1.6]$
(%i6) p2: [0,1.6]$
(%i7) p3: [0,0.44]$
(%i8) p4: [0,0]$
(%i9) w: [85,92,99,100]$
(%i10) ifs(w, [a1,a2,a3,a4], [p1,p2,p3,p4], [5,0], 50000, [style,dots]);

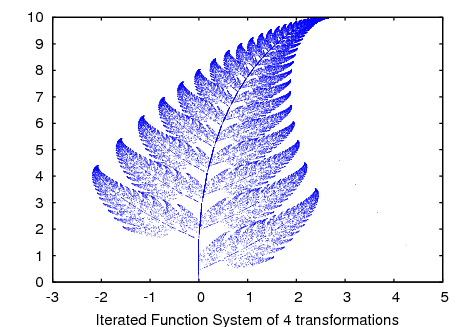Categories: Package dynamics · Plotting ·

Function: orbits (F, y0, n1, n2, [x, x0, xf, xstep], options, …); ¶

Draws the orbits diagram for a family of one-dimensional discrete dynamical systems, with one parameter x; that kind of diagram is used to study the bifurcations of an one-dimensional discrete system.

The function F(y) defines a sequence with a starting value of y0, as in the case of the function evolution, but in this case that function will also depend on a parameter x that will take values in the interval from x0 to xf with increments of xstep. Each value used for the parameter x is shown on the horizontal axis. The vertical axis will show the n2 values of the sequence y(n1+1),..., y(n1+n2+1) obtained after letting the sequence evolve n1 iterations. In addition to the options accepted by plot2d, it accepts an option pixels that sets up the maximum number of different points that will be represented in the vertical direction.

Example. Orbits diagram of the quadratic map, with a parameter a:

(%i1) orbits(x^2+a, 0, 50, 200, [a, -2, 0.25], [style, dots]);

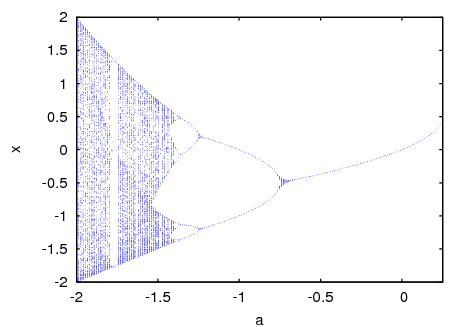
To enlarge the region around the lower bifurcation near x = -1.25 use:

(%i2) orbits(x^2+a, 0, 100, 400, [a,-1,-1.53], [x,-1.6,-0.8],
             [nticks, 400], [style,dots]);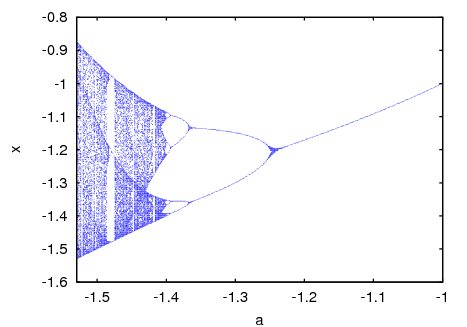

Categories: Package dynamics · Plotting ·

Function: staircase (F, y0, n,options,…); ¶

Draws a staircase diagram for the sequence defined by the recurrence relation

        y(n+1) = F(y(n))

The interpretation and allowed values of the input parameters is the same as for the function evolution. A staircase diagram consists of a plot of the function F(y), together with the line G(y) = y. A vertical segment is drawn from the point (y0, y0) on that line until the point where it intersects the function F. From that point a horizontal segment is drawn until it reaches the point (y1, y1) on the line, and the procedure is repeated n times until the point (yn, yn) is reached. The options are the same as for plot2d.

Example.

(%i1) staircase(cos(y), 1, 11, [y, 0, 1.2]);

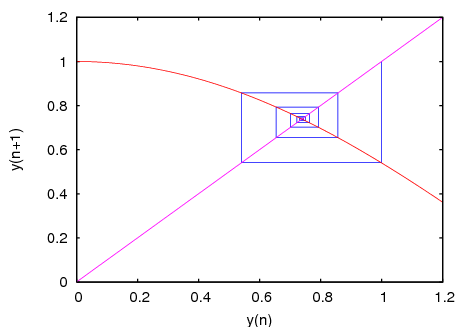Categories: Package dynamics · Plotting ·

56.3 Visualization with VTK

Function scene creates 3D images and animations using the Visualization ToolKit (VTK) software. In order to use that function, Xmaxima and VTK should be installed in your system (including the TCL bindings of VTK, which in some system might come in a separate package).

Function: scene (objects, …, options, …); ¶

Accepts an empty list or a list of several objects and options. The program launches Xmaxima, which opens an external window representing the given objects in a 3-dimensional space and applying the options given. Each object must belong to one of the following 4 classes: sphere, cube, cylinder or cone (see Scene objects). Objects are identified by giving their name or by a list in which the first element is the class name and the following elements are options for that object.

Example. A hexagonal pyramid with a blue background:

(%i1) scene(cone, [background,"#9980e5"])$

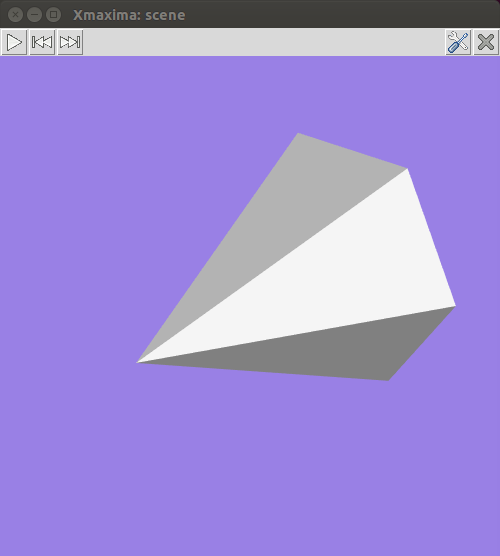
By holding down the left button of the mouse while it is moved on the graphics window, the camera can be rotated showing different views of the pyramid. The two plot options elevation and azimuth can also be used to change the initial orientation of the viewing camera. The camera can be moved by holding the middle mouse button while moving it and holding the right-side mouse button while moving it up or down will zoom in or out.

Each object option should be a list starting with the option name, followed by its value. The list of allowed options can be found in the Scene object's options section.

Example. This will show a sphere falling to the ground and bouncing off without losing any energy. To start or pause the animation, press the play/pause button.

(%i1) p: makelist ([0,0,2.1- 9.8*t^2/2], t, 0, 0.64, 0.01)$

(%i2) p: append (p, reverse(p))$

(%i3) ball: [sphere, [radius,0.1], [thetaresolution,20],
  [phiresolution,20], [position,0,0,2.1], [color,red],
  [animate,position,p]]$

(%i4) ground: [cube, [xlength,2], [ylength,2], [zlength,0.2],
  [position,0,0,-0.1],[color,violet]]$

(%i5) scene (ball, ground, restart)$

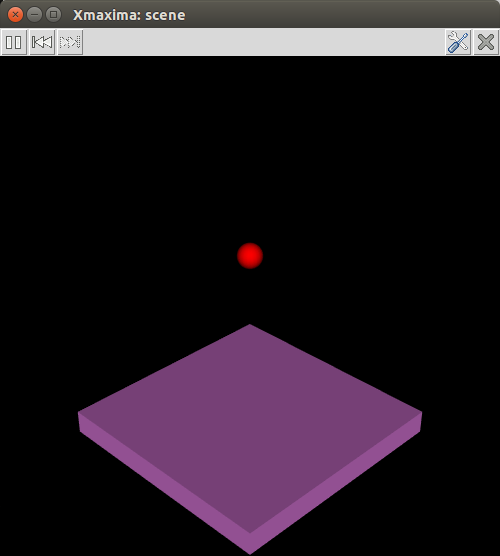
The restart option was used to make the animation restart automatically every time the last point in the position list is reached. The accepted values for the colors are the same as for the color option of plot2d.

Categories: Package dynamics · Plotting ·

Scene options
Scene objects
Scene object’s options

56.3.1 Scene options

Scene option: azimuth [azimuth, angle] ¶

Default value: 135

The rotation of the camera on the horizontal (x, y) plane. angle must be a real number; an angle of 0 means that the camera points in the direction of the y axis and the x axis will appear on the right.

Categories: Package dynamics · Plotting ·

Scene option: background [background, color] ¶

Default value: black

The color of the graphics window’s background. It accepts color names or hexadecimal red-green-blue strings (see the color option of plot2d).

Categories: Package dynamics · Plotting ·

Scene option: elevation [elevation, angle] ¶

Default value: 30

The vertical rotation of the camera. The angle must be a real number; an angle of 0 means that the camera points on the horizontal, and the default angle of 30 means that the camera is pointing 30 degrees down from the horizontal.

Categories: Package dynamics · Plotting ·

Scene option: height [height, pixels] ¶

Default value: 500

The height, in pixels, of the graphics window. pixels must be a positive integer number.

Categories: Package dynamics · Plotting ·

Scene option: restart [restart, value] ¶

Default value: false

A true value means that animations will restart automatically when the end of the list is reached. Writing just “restart” is equivalent to [restart, true].

Categories: Package dynamics · Plotting ·

Scene option: tstep [tstep, time] ¶

Default value: 10

The amount of time, in mili-seconds, between iterations among consecutive animation frames. time must be a real number.

Categories: Package dynamics · Plotting ·

Scene option: width [width, pixels] ¶

Default value: 500

The width, in pixels, of the graphics window. pixels must be a positive integer number.

Categories: Package dynamics · Plotting ·

Scene option: windowname [windowtitle, name] ¶

Default value: .scene

name must be a string that can be used as the name of the Tk window created by Xmaxima for the scene graphics. The default value .scene implies that a new top level window will be created.

Categories: Package dynamics · Plotting ·

Scene option: windowtitle [windowtitle, name] ¶

Default value: Xmaxima: scene

name must be a string that will be written in the title of the window created by scene.

Categories: Package dynamics · Plotting ·

56.3.2 Scene objects

Scene object: cone [cone, options] ¶

Creates a regular pyramid with height equal to 1 and a hexagonal base with vertices 0.5 units away from the axis. Options height and radius can be used to change those defaults and option resolution can be used to change the number of edges of the base; higher values will make it look like a cone. By default, the axis will be along the x axis, the middle point of the axis will be at the origin and the vertex on the positive side of the x axis; use options orientation and center to change those defaults.

Example. This shows a pyramid that starts rotating around the z axis when the play button is pressed.

(%i1) scene([cone, [orientation,0,30,0], [tstep,100],
   [animate,orientation,makelist([0,30,i],i,5,360,5)]], restart)$

Categories: Package dynamics · Plotting ·

Scene object: cube [cube, options] ¶: A cube with edges of 1 unit and faces parallel to the xy, xz and yz planes. The lengths of the three edges can be changed with options xlength, ylength and zlength, turning it into a rectangular box and the faces can be rotated with option orientation.

Categories: Package dynamics · Plotting ·

Scene object: cylinder [cylinder, options] ¶: Creates a regular prism with height equal to 1 and a hexagonal base with vertices 0.5 units away from the axis. Options height and radius can be used to change those defaults and option resolution can be used to change the number of edges of the base; higher values will make it look like a cylinder. The default height can be changed with the option height. By default, the axis will be along the x axis and the middle point of the axis will be at the origin; use options orientation and center to change those defaults.

Categories: Package dynamics · Plotting ·

Scene object: sphere [sphere, options] ¶: A sphere with default radius of 0.5 units and center at the origin.

Categories: Package dynamics · Plotting ·

56.3.3 Scene object’s options

Object option: animation [animation, property, positions] ¶

property should be one of the following 4 object’s properties: origin, scale, position or orientation and positions should be a list of points. When the play button is pressed, the object property will be changed sequentially through all the values in the list, at intervals of time given by the option tstep. The rewind button can be used to point at the start of the sequence making the animation restart after the play button is pressed again.