97 Package trigtools ¶
Trigtools Package
97.1 Introduction to trigtools ¶
We use open-source computer algebra system(CAS) maxima 5.31.2. The trigtools package10 contains commands that help you work with trigonometric expessions. List of functions in trigtools package:
97.2 Functions and Variables for trigtools ¶
- Convert to sin and cos
- Convert to Trignometric Functions
- Convert to Hyperbolic Functions
- Factor Sums of sin and cos Functions
- Solve Trignometric Equations
- Evaluation of Trignometric Functions
- Contract atan Functions
97.2.1 Convert to sin and cos ¶
- Function: c2sin (x) ¶
- Function: c2cos (x) ¶
The function c2sin converts the expression \(a\cos x + b\sin x\) to \(r\sin(x+\phi).\)
The function c2cos converts the expression \(a\cos x + b\sin x\) to \(r\cos(x-\phi).\)
load("trigtools")loads these functions.Examples:
(%i1) load("trigtools")$ (%i2) c2sin(3*sin(x)+4*cos(x)); 4 (%o2) 5 sin(x + atan(-)) 3 (%i3) trigexpand(%),expand; (%o3) 3 sin(x) + 4 cos(x)(%i4) c2cos(3*sin(x)-4*cos(x)); 3 (%o4) - 5 cos(x + atan(-)) 4(%i5) trigexpand(%),expand; (%o5) 3 sin(x) - 4 cos(x)
(%i6) c2sin(sin(x)+cos(x)); %pi (%o6) sqrt(2) sin(x + ---) 4(%i7) trigexpand(%),expand; (%o7) sin(x) + cos(x) (%i8) c2cos(sin(x)+cos(x)); %pi (%o8) sqrt(2) cos(x - ---) 4(%i9) trigexpand(%),expand; (%o9) sin(x) + cos(x)
Example. Solve trigonometric equation
(%i10) eq:3*sin(x)+4*cos(x)=2; (%o10) 3 sin(x) + 4 cos(x) = 2
(%i11) plot2d([3*sin(x)+4*cos(x),2],[x,-%pi,%pi]);
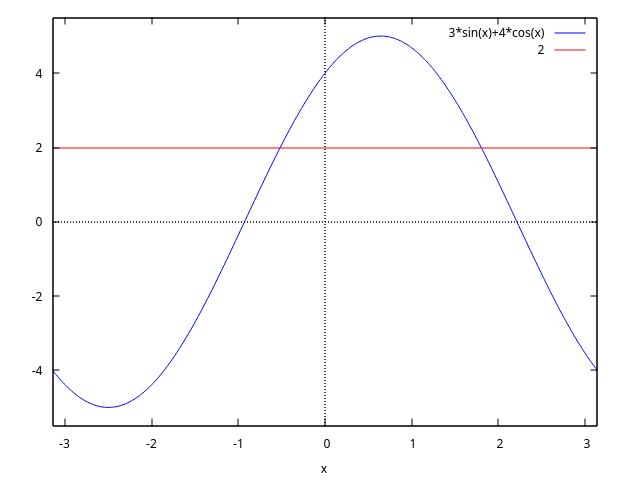
(%i12) eq1:c2sin(lhs(eq))=2; 4 (%o35) 5 sin(x + atan(-)) = 2 3 (%i13) solvetrigwarn:false$ (%i14) solve(eq1)[1]$ x1:rhs(%); 2 4 (%o15) asin(-) - atan(-) 5 3 (%i16) float(%), numer; (%o39) - 0.5157783719341241 (%i17) eq2:c2cos(lhs(eq))=2; 3 (%o17) 5 cos(x - atan(-)) = 2 (%i18) solve(eq2,x)[1]$ x2:rhs(%); 3 2 (%o19) atan(-) + acos(-) 4 5 (%i20) float(%), numer; (%o20) 1.802780589520693 (%i21) sol:[x1,x2]; 2 4 3 2 (%o44) [asin(-) - atan(-), atan(-) + acos(-)] 5 3 4 5Answ.: \(x = x_1 + 2\pi k,\) \(x_1 = \sin^{-1}{2\over 5} - \tan^{-1}{4\over 3},\) or \(x_1 = \tan^{-1}{3\over 4} + \cos^{-1}{2\over 5},\) for \(k\) any integer.
97.2.2 Convert to Trignometric Functions ¶
- Function: c2trig (x) ¶
The function c2trig (convert to trigonometric) reduce expression with hyperbolic functions sinh, cosh, tanh, coth to trigonometric expression with sin, cos, tan, cot.
load("trigtools")loads these functions.Examples:
-
(%i1) load(trigtools)$ (%i2) sinh(x)=c2trig(sinh(x)); cosh(x)=c2trig(cosh(x)); tanh(x)=c2trig(tanh(x)); coth(x)=c2trig(coth(x)); (%o2) sinh(x) = - %i sin(%i x) (%o3) cosh(x) = cos(%i x) (%o4) tanh(x) = - %i tan(%i x) (%o5) coth(x) = %i cot(%i x)
- see http://www.math.utexas.edu/pipermail/maxima/2013/034585.html
(%i6) cos(p+q*%i); (%o6) cos(%i q + p) (%i7) trigexpand(%); (%o7) cos(p) cosh(q) - %i sin(p) sinh(q) (%i8) c2trig(%); (%o8) cos(%i q + p)
-
(%i9) sin(a+b*%i); (%o9) sin(%i b + a) (%i10) trigexpand(%); (%o10) %i cos(a) sinh(b) + sin(a) cosh(b) (%i11) c2trig(%); (%o11) sin(%i b + a)
-
(%i12) cos(a*%i+b*%i); (%o12) cos(%i b + %i a) (%i13) trigexpand(%); (%o13) sinh(a) sinh(b) + cosh(a) cosh(b) (%i14) c2trig(%); (%o14) cos(%i b + %i a)
-
(%i15) tan(a+%i*b); (%o15) tan(%i b + a)
(%i16) trigexpand(%); %i tanh(b) + tan(a) (%o16) --------------------- 1 - %i tan(a) tanh(b)(%i17) c2trig(%); (%o217) tan(%i b + a)
-
(%i18) cot(x+%i*y); (%o18) cot(%i y + x) (%i19) trigexpand(%); (- %i cot(x) coth(y)) - 1 (%o19) ------------------------- cot(x) - %i coth(y) (%i20) c2trig(%); (%o20) cot(%i y + x)
Categories: Trigonometric functions · Package trigtools ·-
97.2.3 Convert to Hyperbolic Functions ¶
- Function: c2hyp (x) ¶
The function c2hyp (convert to hyperbolic) convert expression with exp function to expression with hyperbolic functions sinh, cosh.
load("trigtools")loads this function.Examples:
(%i6) c2hyp(exp(x)); (%o6) sinh(x) + cosh(x) (%i7) c2hyp(exp(x)+exp(x^2)+1); 2 2 (%o7) sinh(x ) + cosh(x ) + sinh(x) + cosh(x) + 1 (%i8) c2hyp(exp(x)/(2*exp(y)-3*exp(z))); sinh(x) + cosh(x) (%o8) --------------------------------------------- 2 (sinh(y) + cosh(y)) - 3 (sinh(z) + cosh(z))
97.2.4 Factor Sums of sin and cos Functions ¶
- Function: trigfactor (x) ¶
The function trigfactor factors expresions of form \(\pm \sin x \pm \cos y.\)
load("trigtools")loads this function.Examples:
-
(%i2) trigfactor(sin(x)+cos(x)); %pi (%o2) sqrt(2) cos(x - ---) 4 (%i3) trigrat(%); (%o3) sin(x) + cos(x) -
(%i4) trigfactor(sin(x)+cos(y)); y x %pi y x %pi (%o4) 2 cos(- - - + ---) cos(- + - - ---) 2 2 4 2 2 4(%i5) trigrat(%); (%o5) cos(y) + sin(x)
-
(%i6) trigfactor(sin(x)-cos(3*y)); 3 y x %pi 3 y x %pi (%o6) 2 sin(--- - - + ---) sin(--- + - - ---) 2 2 4 2 2 4 (%i7) trigrat(%); (%o7) sin(x) - cos(3 y) -
(%i8) trigfactor(-sin(5*x)-cos(3*y)); 3 y 5 x %pi 3 y 5 x %pi (%o8) - 2 cos(--- - --- + ---) cos(--- + --- - ---) 2 2 4 2 2 4 (%i9) trigrat(%); (%o9) (- cos(3 y)) - sin(5 x) -
(%i10) sin(alpha)+sin(beta)=trigfactor(sin(alpha)+sin(beta)); beta alpha beta alpha (%o10) sin(beta) + sin(alpha) = 2 cos(---- - -----) sin(---- + -----) 2 2 2 2(%i11) trigrat(%); (%o78) sin(beta) + sin(alpha) = sin(beta) + sin(alpha)
-
(%i12) sin(alpha)-sin(beta)=trigfactor(sin(alpha)-sin(beta)); beta alpha beta alpha (%o12) sin(alpha) - sin(beta) = - 2 sin(---- - -----) cos(---- + -----) 2 2 2 2 -
(%i13) cos(alpha)+cos(beta)=trigfactor(cos(alpha)+cos(beta)); beta alpha beta alpha (%o80) cos(beta) + cos(alpha) = 2 cos(---- - -----) cos(---- + -----) 2 2 2 2 -
(%i14) cos(alpha)-cos(beta)=trigfactor(cos(alpha)-cos(beta)); beta alpha beta alpha (%o14) cos(alpha) - cos(beta) = 2 sin(---- - -----) sin(---- + -----) 2 2 2 2 -
(%i15) trigfactor(3*sin(x)+7*cos(x)); (%o15) 3 sin(x) + 7 cos(x)
(%i16) c2sin(%); 7 (%o16) sqrt(58) sin(x + atan(-)) 3(%i17) trigexpand(%),expand; (%o17) 3 sin(x) + 7 cos(x)
10.
(%i18) trigfactor(sin(2*x)); (%o18) sin(2 x) (%i19) trigexpand(%); (%o19) 2 cos(x) sin(x)
Categories: Trigonometric functions · Package trigtools ·-
97.2.5 Solve Trignometric Equations ¶
- Function: trigsolve (x) ¶
The function trigsolve find solutions of trigonometric equation from interval \([a,b).\)
load("trigtools")loads this function.Examples:
-
(%i38) eq:eq:3*sin(x)+4*cos(x)=2; (%o38) 3 sin(x) + 4 cos(x) = 2 (%i39) plot2d([3*sin(x)+4*cos(x),2],[x,-%pi,%pi]);
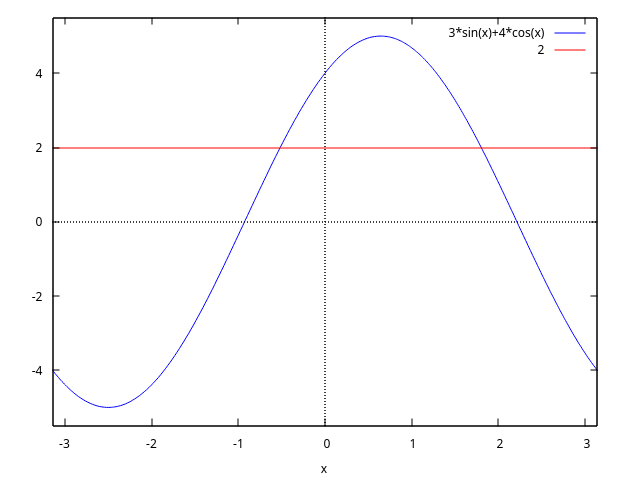
(%o39) (%i40) sol:trigsolve(eq,-%pi,%pi); 2 sqrt(21) 12 2 sqrt(21) 12 (%o40) {atan(---------- - --), %pi - atan(---------- + --)} 5 5 5 5 (%i41) float(%), numer; (%o41) {- 0.5157783719341241, 1.802780589520693}Answ. : \(x = \tan^{-1}\left({2\sqrt{21}\over 5} - {12\over 5}\right) + 2\pi k\) ; \(x = \pi - \tan^{-1}\left({2\sqrt{21}\over 5} + {12\over 5}\right) + 2\pi k,\) \(k\) – any integer.
-
(%i6) eq:cos(3*x)-sin(x)=sqrt(3)*(cos(x)-sin(3*x)); (%o6) cos(3 x) - sin(x) = sqrt(3) (cos(x) - sin(3 x)) (%i7) plot2d([lhs(eq)-rhs(eq)], [x,0,2*%pi])$
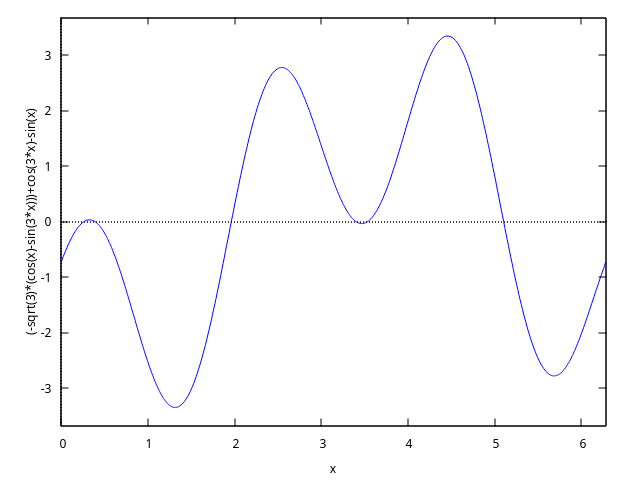
We have 6 solutions from [0, 2*pi].
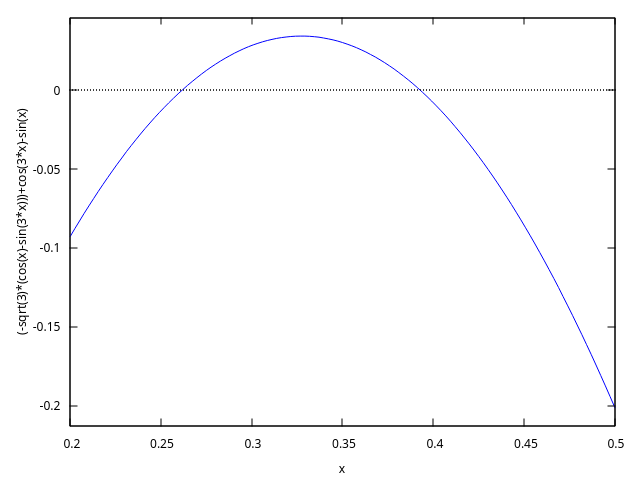
(%i8) plot2d([lhs(eq)-rhs(eq)], [x,0.2,0.5]);
(%i9) plot2d([lhs(eq)-rhs(eq)], [x,3.3,3.6]);
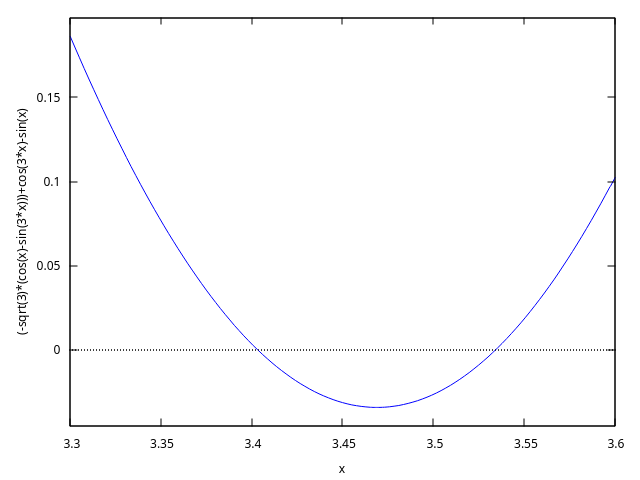
(%i10) trigfactor(lhs(eq))=map(trigfactor,rhs(eq)); %pi %pi %pi %pi (%o15) - 2 sin(x + ---) sin(2 x - ---) = 2 sqrt(3) sin(x - ---) sin(2 x - ---) 4 4 4 4 (%i11) factor(lhs(%)-rhs(%)); 4 x + %pi 4 x - %pi 8 x - %pi (%o11) - 2 (sin(---------) + sqrt(3) sin(---------)) sin(---------) 4 4 4Equation is equivalent to
(%i12) L:factor(rhs(%)-lhs(%)); 4 x + %pi 4 x - %pi 8 x - %pi (%o12) 2 (sin(---------) + sqrt(3) sin(---------)) sin(---------) 4 4 4(%i13) eq1:part(L,2)=0; 4 x + %pi 4 x - %pi (%o13) sin(---------) + sqrt(3) sin(---------) = 0 4 4(%i14) eq2:part(L,3)=0; 8 x - %pi (%o14) sin(---------) = 0 4(%i15) S1:trigsolve(eq1,0,2*%pi); %pi 13 %pi (%o15) {---, ------} 12 12 (%i16) S2:trigsolve(eq2,0,2*%pi); %pi 5 %pi 9 %pi 13 %pi (%o16) {---, -----, -----, ------} 8 8 8 8 (%i17) S:listify(union(S1,S2)); %pi %pi 5 %pi 13 %pi 9 %pi 13 %pi (%o17) [---, ---, -----, ------, -----, ------] 12 8 8 12 8 8 (%i18) float(%), numer; (%o18) [0.2617993877991494, 0.3926990816987241, 1.963495408493621, 3.403392041388942, 3.534291735288517, 5.105088062083414]Answer: \(x = a + 2\pi k,\) where \(a\) any from \(S\), \(k\) any integer.
-
(%i19) eq:8*cos(x)*cos(4*x)*cos(5*x)-1=0; (%o19) 8 cos(x) cos(4 x) cos(5 x) - 1 = 0 (%i20) trigrat(%); (%o20) 2 cos(10 x) + 2 cos(8 x) + 2 cos(2 x) + 1 = 0
Left side is periodic with period \(T=\pi.\)
We have 10 solutions from [0, pi].
(%i21) plot2d([lhs(eq),rhs(eq)],[x,0,%pi]);
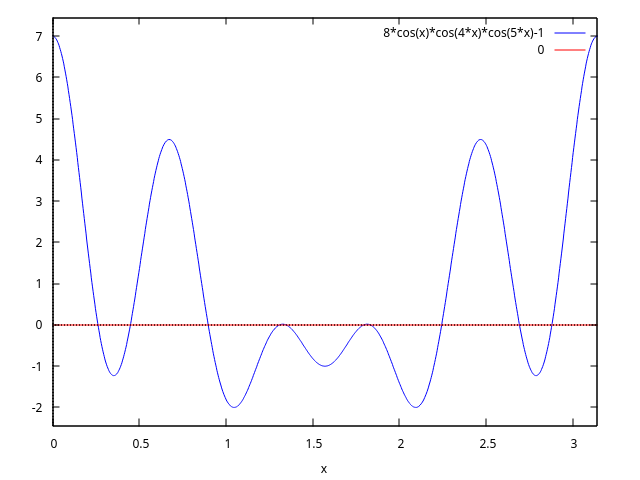
(%i22) x4:find_root(eq, x, 1.3, 1.32); (%o22) 1.308996938995747 (%i23) x5:find_root(eq, x, 1.32, 1.35); (%o23) 1.346396851538483 (%i24) plot2d([lhs(eq),0], [x,1.3,1.35], [gnuplot_preamble, "set grid;"]);
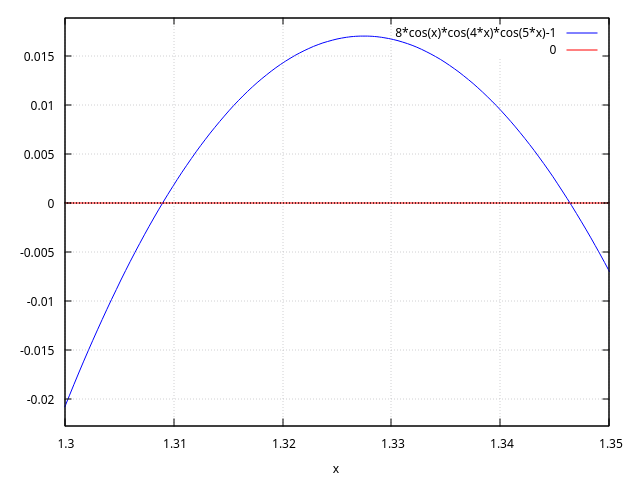
Equation we multiply by \(2\sin x\cos 2x:\)
(%i25) eq*2*sin(x)*cos(2*x); (%o25) 2 sin(x) cos(2 x) (8 cos(x) cos(4 x) cos(5 x) - 1) = 0 (%i26) eq1:trigreduce(%),expand; (%o26) sin(13 x) + sin(x) = 0
(%i27) trigfactor(lhs(eq1))=0; (%o27) 2 cos(6 x) sin(7 x) = 0
(%i28) S1:trigsolve(cos(6*x),0,%pi); %pi %pi 5 %pi 7 %pi 3 %pi 11 %pi (%o28) {---, ---, -----, -----, -----, ------} 12 4 12 12 4 12(%i29) S2:trigsolve(sin(7*x),0,%pi); %pi 2 %pi 3 %pi 4 %pi 5 %pi 6 %pi (%o29) {0, ---, -----, -----, -----, -----, -----} 7 7 7 7 7 7We remove solutions of \(\sin x = 0\) and \(\cos 2x = 0.\)
(%i30) S3:trigsolve(sin(x),0,%pi); (%o30) {0} (%i31) S4:trigsolve(cos(2*x),0,%pi); %pi 3 %pi (%o31) {---, -----} 4 4We find 10 solutions from \([0, \pi]:\)
(%i32) union(S1,S2)$ setdifference(%,S3)$ setdifference(%,S4); %pi %pi 2 %pi 5 %pi 3 %pi 4 %pi 7 %pi 5 %pi 6 %pi 11 %pi (%o34) {---, ---, -----, -----, -----, -----, -----, -----, -----, ------} 12 7 7 12 7 7 12 7 7 12(%i35) S:listify(%); %pi %pi 2 %pi 5 %pi 3 %pi 4 %pi 7 %pi 5 %pi 6 %pi 11 %pi (%o35) [---, ---, -----, -----, -----, -----, -----, -----, -----, ------] 12 7 7 12 7 7 12 7 7 12(%i36) length(S); (%o36) 10 (%i37) float(S), numer; (%o37) [0.2617993877991494, 0.4487989505128276, 0.8975979010256552, 1.308996938995747, 1.346396851538483, 1.79519580205131, 1.832595714594046, 2.243994752564138, 2.692793703076966, 2.879793265790644]
Answer: \(x = a + 2\pi k,\) where \(a\) any from \(S\), \(k\) any integer.
Categories: Trigonometric functions · Package trigtools ·-
97.2.6 Evaluation of Trignometric Functions ¶
- Function: trigvalue (x) ¶
The function trigvalue compute values of \(\sin {m\pi\over n},\) \(\cos {m\pi\over n},\) \(\tan {m\pi\over n},\) and \(\cot {m\pi\over n}\) in radicals.
trigvalueis essentially an internal function. Use functiontrigevalin preference.load("trigtools")loads this function.
- Function: trigeval (x) ¶
The function trigeval compute values of expressions with \(\sin {m\pi\over n},\) \(\cos {m\pi\over n},\) \(\tan {m\pi\over n},\) and \(\cot {m\pi\over n}\) in radicals.
load("trigtools") loads this function.
Examples:
- Values of trignometric functions
(%i1) load(trigtools)$
(%i2) trigvalue(sin(%pi/10)); sqrt(5) - 1 (%o2) ----------- 4(%i3) trigvalue(cos(%pi/10)); sqrt(sqrt(5) + 5) (%o3) ----------------- 3/2 2(%i4) trigvalue(tan(%pi/10)); sqrt(5 - 2 sqrt(5)) (%o4) ------------------- sqrt(5)(%i5) float(%), numer; (%o5) 0.3249196962329063 (%i6) float(tan(%pi/10)), numer; (%o6) 0.3249196962329063 (%i7) trigvalue(cot(%pi/10)); (%o7) sqrt(2 sqrt(5) + 5) (%i8) float(%), numer; (%o8) 3.077683537175254 (%i9) float(cot(%pi/10)), numer; (%o9) 3.077683537175254 (%i10) trigvalue(sin(%pi/32)); sqrt(2 - sqrt(sqrt(sqrt(2) + 2) + 2)) (%o10) ------------------------------------- 2 (%i11) trigvalue(cos(%pi/32)); sqrt(sqrt(sqrt(sqrt(2) + 2) + 2) + 2) (%o11) ------------------------------------- 2 (%i12) trigvalue(cos(%pi/256)); sqrt(sqrt(sqrt(sqrt(sqrt(sqrt(sqrt(2) + 2) + 2) + 2) + 2) + 2) + 2) (%o12) ------------------------------------------------------------------- 2 (%i13) trigvalue(cos(%pi/60)); sqrt(sqrt(sqrt(2) sqrt(3) sqrt(sqrt(5) + 5) + sqrt(5) + 7) + 4) (%o13) --------------------------------------------------------------- 3/2 2(%i14) trigvalue(sin(%pi/60)); sqrt(4 - sqrt(sqrt(2) sqrt(3) sqrt(sqrt(5) + 5) + sqrt(5) + 7)) (%o14) --------------------------------------------------------------- 3/2 2(%i15) trigvalue(sin(%pi/18)); %pi (%o15) sin(---) 18(%i16) trigvalue(sin(%pi/20)); sqrt(4 - sqrt(2) sqrt(sqrt(5) + 5)) (%o16) ----------------------------------- 3/2 2 - ode example
(%i17) load(odes)$
(%i18) eq:'diff(y,x,5)+2*y=0; 5 d y (%o18) --- + 2 y = 0 5 dx(%i19) odeL(eq,y,x);
1/5 4 %pi - 2 cos(-----) x 5 1/5 4 %pi (%o19) y = C5 %e sin(2 sin(-----) x) 5 1/5 4 %pi - 2 cos(-----) x 5 1/5 4 %pi + C4 %e cos(2 sin(-----) x) 5 1/5 2 %pi - 2 cos(-----) x 5 1/5 2 %pi + C3 %e sin(2 sin(-----) x) 5 1/5 2 %pi - 2 cos(-----) x 1/5 5 1/5 2 %pi - 2 x + C2 %e cos(2 sin(-----) x) + C1 %e 5(%i20) sol:trigeval(%); (sqrt(5) - 1) x - --------------- 9/5 2 sqrt(sqrt(5) + 5) x (%o20) y = C3 %e sin(-------------------) 13/10 2 (sqrt(5) - 1) x - --------------- 9/5 2 sqrt(sqrt(5) + 5) x + C2 %e cos(-------------------) 13/10 2 (sqrt(5) + 1) x --------------- 9/5 2 sqrt(5 - sqrt(5)) x + C5 %e sin(-------------------) 13/10 2 (sqrt(5) + 1) x --------------- 9/5 1/5 2 sqrt(5 - sqrt(5)) x - 2 x + C4 %e cos(-------------------) + C1 %e 13/10 2(%i21) subst(sol,eq)$ (%i22) ev(%, nouns)$ (%i23) radcan(%); (%o23) 0 = 0
- n-th root of complex number
Example. Find the 4-th roots of %i
(%i24) solve(x^4=%i,x); 1/8 1/8 1/8 1/8 (%o24) [x = (- 1) %i, x = - (- 1) , x = - (- 1) %i, x = (- 1) ](%i25) rectform(%); %pi %pi %pi %pi (%o25) [x = %i cos(---) - sin(---), x = (- %i sin(---)) - cos(---), 8 8 8 8 %pi %pi %pi %pi x = sin(---) - %i cos(---), x = %i sin(---) + cos(---)] 8 8 8 8(%i26) trigeval(%); sqrt(sqrt(2) + 2) %i sqrt(2 - sqrt(2)) (%o26) [x = -------------------- - -----------------, 2 2 sqrt(2 - sqrt(2)) %i sqrt(sqrt(2) + 2) x = (- --------------------) - -----------------, 2 2 sqrt(2 - sqrt(2)) sqrt(sqrt(2) + 2) %i x = ----------------- - --------------------, 2 2 sqrt(2 - sqrt(2)) %i sqrt(sqrt(2) + 2) x = -------------------- + -----------------] 2 2
97.2.7 Contract atan Functions ¶
- Function: atan_contract (r) ¶
The function atan_contract(r) contracts atan functions. We assume: \(|r| < {\pi\over 2}.\)
load("trigtools")loads this function.Examples:
(%i1) load(trigtools)$
-
(%i2) atan_contract(atan(x)+atan(y)); (%o2) atan(y) + atan(x) (%i3) assume(abs(atan(x)+atan(y))<%pi/2)$ (%i4) atan(x)+atan(y)=atan_contract(atan(x)+atan(y)); y + x (%o4) atan(y) + atan(x) = atan(-------) 1 - x y -
(%i5) atan(1/3)+atan(1/5)+atan(1/7)+atan(1/8)$ %=atan_contract(%); 1 1 1 1 %pi (%o6) atan(-) + atan(-) + atan(-) + atan(-) = --- 3 5 7 8 4 - Machin’s formulae
(%i7) 4*atan(1/5)-atan(1/239)=atan_contract(4*atan(1/5)-atan(1/239)); 1 1 %pi (%o7) 4 atan(-) - atan(---) = --- 5 239 4 - see http://en.wikipedia.org/wiki/Machin-like_formula
(%i8) 12*atan(1/49)+32*atan(1/57)-5*atan(1/239)+12*atan(1/110443)$ %=atan_contract(%); 1 1 1 1 %pi (%o9) 12 atan(--) + 32 atan(--) - 5 atan(---) + 12 atan(------) = --- 49 57 239 110443 4
Categories: Trigonometric functions · Package trigtools ·-