Package colnew (Maxima 5.47post Manual)

48 Package colnew

Introduction to colnew
Functions and Variables for colnew
Examples for colnew
References for colnew

48.1 Introduction to colnew

colnew solves mixed-order systems of boundary-value problems (BVPs) in ordinary differential equations(ODEs). It is a Common Lisp translation (via f2cl) of the Fortran routine COLNEW (see Bader&Ascher 1987).

The method uses collocation at Gaussian points and interpolation using basis functions. Approximate solutions are computed on a sequence of automatically selected meshes until a user-specified set of tolerances is satisfied. A damped Newton’s method is used for the nonlinear iteration.

COLNEW has some advanced features:

Continuation: Most iterative numerical solvers require an initial guess. There are parameter dependent problems that have an obvious solution for a special value of the parameter (for example a coupling constant vanishes). One can then slowly vary the parameter, solving the problem numerically using as a guess the previous solution, until one gets into a strong coupling regime, hence the name continuation. Sometimes an artificial parameter is introduced to allow the use of continuation.
Singularities: Another interesting feature of COLNEW is that one can manage singularities in the differential equation by setting interior "boundary points" on the singularities. This is because the differential equation is only imposed in the interior of the intervals, but the solution is checked for continuity and continuity of the derivative on the boundary of the intervals.
Stiff differential equations: COLNEW can be used for solving some stiff differential equations due to the use of adaptive meshes.

The maxima interface to COLNEW exposes the full power and complexity of the Fortran 77 implementation.

COLNEW is a modification of the package COLSYS (see Ascher 1981a and Ascher 1981b). It incorporates a new basis representation replacing B-splines, and improvements for the linear and nonlinear algebraic equation solvers. The package can be referenced as either COLNEW or COLSYS.

Many practical problems that are not in the standard form accepted by COLNEW can be converted into this form. See Asher&Russell 1981.

Categories: Numerical methods · Differential equations · Share packages · Package colnew ·

48.2 Functions and Variables for colnew

Function: colnew_expert
colnew_expert (ncomp, m, aleft, aright, zeta, ipar, ltol, tol, fixpnt, ispace, fspace, iflag, fsub, dfsub, gsub, dgsub, guess) ¶

colnew_expert solves mixed-order systems of boundary-value problems (BVPs) in ordinary differential equations (ODEs) using a numerical collocation method.

colnew_expert returns the list [iflag, fspace, ispace]. iflag is an error flag. Lists fspace and ispace contain the state of the solution and can be: used by colnew_appsln to calculate solution values at arbitrary points in the solution domain; and passed back to colnew_expert to restart the solution process with different arguments.

The function arguments are:

ncomp

Number of differential equations (ncomp ≤ 20)

m

Integer list of length ncomp. m[j] is the order of the j-th differential equation, with 1 ≤ m[j] ≤ 4 and mstar = sum(m[j]) ≤ 40.

aleft

Left end of interval

aright

Right end of interval

zeta

Real list of length mstar. zeta[j] is the j-th boundary or side condition point. The list zeta must be ordered, with zeta[j] ≤ zeta[j+1]. All side condition points must be mesh points in all meshes used, see description of ipar[11] and fixpnt below.

ipar

A integer list of length 11. The parameters in ipar are:

ipar[1]
- 0, if the problem is linear
- 1, if the problem is nonlinear
ipar[2] ( = k )
Number of collocation points per subinterval , where max(m[i]) ≤ k ≤ 7.
If ipar[2]=0 then colnew sets k = max(max(m[i])+1, 5-max(m[i]))
ipar[3] ( = n )
Number of subintervals in the initial mesh.
If ipar[3] = 0 then colnew arbitrarily sets n = 5.
ipar[4] ( = ntol )
Number of solution and derivative tolerances.
Require 0 < ntol ≤ mstar.
ipar[5] ( = ndimf )
The length of list fspace. Its size provides a constraint on nmax. Choose ipar[5] according to the formula ipar[5] ≥ nmax*nsizef where nsizef = 4 + 3 * mstar + (5+kd) * kdm + (2*mstar-nrec) * 2*mstar.
ipar[6] ( = ndimi )
The length of list ispace. Its size provides a constraint on nmax, the maximum number of subintervals. Choose ipar[6] according to the formula ipar[6] ≥ nmax*nsizei where nsizei = 3 + kdm with kdm = kd + mstar
kd = k * ncomp
nrec = number of right end boundary conditions.
ipar[7] ( = iprint )
output control
- -1, for full diagnostic printout
- 0, for selected printout
- 1, for no printout
ipar[8] ( = iread )
- 0, causes colnew to generate a uniform initial mesh.
- 1, if the initial mesh is provided by the user. it is defined in fspace as follows: the mesh aleft=x[1]<x[2]< ... <x[n]<x[n+1]=aright will occupy fspace[1], ..., fspace[n+1]. the user needs to supply only the interior mesh points fspace[j] = x[j], j = 2, ..., n.
- 2, if the initial mesh is supplied by the user as with ipar[8]=1, and in addition no adaptive mesh selection is to be done.
ipar[9] ( = iguess )
- 0, if no initial guess for the solution is provided
- 1, if an initial guess is provided by the user in subroutine guess.
- 2, if an initial mesh and approximate solution coefficients are provided by the user in fspace. (the former and new mesh are the same).
- 3, if a former mesh and approximate solution coefficients are provided by the user in fspace, and the new mesh is to be taken twice as coarse; i.e.,every second point from the former mesh.
- 4, if in addition to a former initial mesh and approximate solution coefficients, a new mesh is provided in fspace as well. (see description of output for further details on iguess = 2, 3, and 4.)
ipar[10]
- 0, if the problem is regular
- 1, if the first relax factor is =rstart, and the nonlinear iteration does not rely on past covergence (use for an extra sensitive nonlinear problem only).
- 2, if we are to return immediately upon (a) two successive nonconvergences, or (b) after obtaining error estimate for the first time.
ipar[11] ( = nfxpnt , the dimension of fixpnt)
The number of fixed points in the mesh other than aleft and aright. The code requires that all side condition points other than aleft and aright (see description of zeta) must be included as fixed points in fixpnt.

ltol

A list of length ntol=ipar[4]. ltol[j]=k specifies that the j-th tolerance in tol controls the error in the k-th component of z(u).

The list ltol must be ordered with 1 ≤ ltol[1] < ltol[2] < ... < ltol[ntol] ≤ mstar.

tol

An list of length ntol=ipar[4]. tol[j] is the error tolerance on the ltol[j]-th component of z(u).

Thus, the code attempts to satisfy for j=1,...,ntol on each subinterval abs(z(v)-z(u))[k] ≤ tol(j)*abs(z(u))[k]+tol(j) if v(x) is the approximate solution vector.

fixpnt

An list of length ipar[11]. It contains the points, other than aleft and aright, which are to be included in every mesh. All side condition points other than aleft and aright (see zeta) be included as fixed points in fixpnt.

ispace

An integer work list of length ipar[6].

fspace

A real work list of length ipar[5].

fsub

fsub is a function f(x,z1,...,z[mstar]) which realizes the system of ODEs.

It returns a list of ncomp values, one for each ODE. Each value is the highest order derivative in each ode in terms of of x,z1,...,z[mstar] .

dfsub

dfsub is a function df(x,z1,...,z[mstar]) for evaluating the Jacobian of f.

gsub

Name of subroutine gsub(i,z1,z2,...,z[mstar]) for evaluating the i-th component of the boundary value function g(z1,...,z[mstar]). The independent variable x is not an argument of g. The value x=zeta[i] must be substituted in advance.

dgsub

Name of subroutine dgsub(i,z1,...,z[mstar]) for evaluating the i-th row of the Jacobian of g(z1,...,z[mstar]).

guess

Name of subroutine to evaluate the initial approximation for (u(x)) and for dmval(u(x))= vector of the mj-th derivatives of u(x). This subroutine is needed only if using ipar(9) = 1.

The return value of colnew_expert is the list [iflag, fspace, ispace], where:

iflag

The mode of return from colnew_expert.

= 1 for normal return
= 0 if the collocation matrix is singular.
= -1 if the expected no. of subintervals exceeds storage specifications.
= -2 if the nonlinear iteration has not converged.
= -3 if there is an input data error.

fspace

A list of floats of length ipar[5].

ispace

A list of integers of length ipar[6].

colnew_appsln uses fspace and ispace to calculate solution values at arbitrary points. The lists can also be used to restart the solution process with modified meshes and parameters.

Categories: Numerical methods · Differential equations · Package colnew ·

Function: colnew_appsln
colnew_appsln (x, zlen, fspace, ispace) ¶

Return a list of solution values from colnew_expert results.

The function arguments are:

x: List of x-coordinates to calculate solution.
zlen: mstar, the length of the solution list z
fspace: List fspace returned from colnew_expert.
ispace: List ispace returned from colnew_expert.

Categories: Numerical methods · Differential equations · Package colnew ·

48.3 Examples for colnew

COLNEW is best learned by example.

Example 1: A uniformly loaded beam of variable stiffness
Example 2: Deformation of a spherical cap
Example 3: Rotating flow of viscous incompressible fluid
Example 4: Quantum Neumann equation
Example 5: Simple example of continuation

48.3.1 Example 1: A uniformly loaded beam of variable stiffness

The problem describes a uniformly loaded beam of variable stiffness, simply supported at both ends.

The problem from Gawain&Ball 1978 and is Example 1 from Ascher 1981a. The maxima code is in file share/colnew/prob1.mac and a Fortran implementation is in share/colnew/ex1.

The differential equation is

(x^3 u'')'' = x^3 u'''' + 6 x^2 u''' + 6x u'' = 1 over 1 ≤ x ≤ 2

with boundary conditions

u(1) = 0, u''(1) = 0, u(2) = 0, u''(2) = 0

The exact solution is

u(x) = (1/4) (10 ln(2) - 3) (1-x) + (1/2) (1/x + (3+x) ln(x) - x)

There is nconc = 1 differential equation of fourth order. The list of orders m = [4] and mstar = sum(m[j]) = 4.

The unknown vector of length mstar is

z(x) = [z_1(x),z_2(x),z_3(x),z_4(x)]

=[u(x),u'(x),u''(x),u'''(x)].

The differential equation is expressed as

u''''(x) = F(x,z_1,z_2,z_3,z_4) = 1 - 6 x^2 z_3 - 6x z_2

There are mstar=4 boundary conditions. They are given by a function G(z_1,z_2,z_3,z_4) that returns a list of length mstar. The j-th boundary condition applies at x = zeta[j] and is satisfied when g[j] = 0. We have

j	zeta[j]	Condition	g[j]
1	1.0	u=0	z_1
2	1.0	u''=0	z_3
3	2.0	u=0	z_1
4	2.0	u''=0	z_3

giving zeta = [1.0,1,0,2.0,2.0] and G(z_1,z_2,z_3,z_4) = [z_1, z_3, z_1, z_3].

The Jacobians df and dg of f and g respectively are determined symbolically.

The solution uses the default five collocation points per subinterval and the first mesh contains only one subinterval. The maximum error magnitude in the approximate solution is evaluated at 100 equidistant points by function colnew_appsln using the results returned by COLNEW and compared to the estimates from the code.

(%i1) load("colnew")$

(%i2) /* One differential equation of order 4 */
 m : [4];

(%o2)                          [4]

(%i3) /* Location of boundary conditions */
 zeta : float([1,1,2,2]);

(%o3)                 [1.0, 1.0, 2.0, 2.0]

(%i4) /* Set up parameter array.  Use defaults for all except as shown */
 ipar : makelist(0,k,1,11);
(%o4)           [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

(%i5) /* initial mesh size */
 ipar[3] : 1$

(%i6) /* number of tolerances */
 ipar[4] : 2$

(%i7) /* size of real work array */
 ipar[5] : 2000$

(%i8) /* size of integer work array */
 ipar[6] : 200$

(%i9) /* Two error tolerances (on u and its second derivative) */
 ltol : [1, 3];
(%o9)                        [1, 3]

(%i10) tol : [1d-7, 1d-7];

(%o10)                  [1.0e-7, 1.0e-7]

(%i11) /* Real work array */
 fspace : makelist(0d0, k, 1, ipar[5])$

(%i12) /* Integer work array */
 ispace : makelist(0, k, 1, ipar[6])$

(%i13) /* no internal fixed points */
 fixpnt : []$

(%i14) /* Define the equations */
 fsub(x, z1, z2, z3, z4) := [(1-6*x^2*z4-6*x*z3)/x^3];
                                          2
                                   1 - 6 x  z4 + (- 6) x z3
(%o14) fsub(x, z1, z2, z3, z4) := [------------------------]
                                               3
                                              x

(%i15) df : jacobian(fsub(x,z1, z2, z3, z4),[z1,z2,z3,z4]);
                       [         6     6 ]
(%o15)                 [ 0  0  - --  - - ]
                       [          2    x ]
                       [         x       ]

(%i16) define(dfsub(x, z1, z2, z3, z4), df);

                                     [         6     6 ]
(%o16)   dfsub(x, z1, z2, z3, z4) := [ 0  0  - --  - - ]
                                     [          2    x ]
                                     [         x       ]

(%i17) g(z1, z2, z3, z4) := [z1, z3, z1, z3];
(%o17)        g(z1, z2, z3, z4) := [z1, z3, z1, z3]

(%i18) gsub(i, z1, z2, z3, z4) :=
 subst(['z1=z1,'z2=z2,'z3=z3,'z4=z4], g(z1, z2, z3, z4)[i]);

(%o18) gsub(i, z1, z2, z3, z4) := 
subst(['z1 = z1, 'z2 = z2, 'z3 = z3, 'z4 = z4], 
g(z1, z2, z3, z4) )
                 i

(%i19) dg:jacobian(g(z1, z2, z3, z4), [z1,z2,z3,z4]);
                         [ 1  0  0  0 ]
                         [            ]
                         [ 0  0  1  0 ]
(%o19)                   [            ]
                         [ 1  0  0  0 ]
                         [            ]
                         [ 0  0  1  0 ]

(%i20) dgsub(i, z1, z2, z3, z4) :=
 subst(['z1=z1,'z2=z2,'z3=z3,'z4=z4], row(dg, i)[1]);

(%o20) dgsub(i, z1, z2, z3, z4) := 
     subst(['z1 = z1, 'z2 = z2, 'z3 = z3, 'z4 = z4], row(dg, i) )
                                                               1

(%i21) /* Exact solution */
  exact(x) := [.25*(10.*log(2.)-3.)*(1.-x) + .5*(1./x+(3.+x)*log(x)-x),
             -.25*(10.*log(2.)-3.) + .5*(-1./x/x+log(x)+(3.+x)/x-1.),
             .5*(2./x**3+1./x-3./x/x),
             .5*(-6./x**4-1./x/x+6./x**3)]$

(%i22) [iflag, fspace, ispace] :
 colnew_expert(1, m, 1d0, 2d0, zeta, ipar, ltol, tol, fixpnt, ispace, fspace,
             0, fsub, dfsub, gsub, dgsub, dummy)$


 VERSION *COLNEW* OF COLSYS .    


 THE MAXIMUM NUMBER OF SUBINTERVALS IS MIN (  12 (ALLOWED FROM FSPACE),  16 (ALLOWED FROM ISPACE) )

 THE NEW MESH (OF    1 SUBINTERVALS), 
    1.000000    2.000000

 THE NEW MESH (OF    2 SUBINTERVALS), 
    1.000000    1.500000    2.000000

 THE NEW MESH (OF    4 SUBINTERVALS), 
    1.000000    1.250000    1.500000    1.750000    2.000000

(%i23) /* Calculate the error at 101 points using the known exact solution */
 block([x : 1,
       err : makelist(0d0, k, 1, 4),
       j],
  for j : 1 thru 101 do
    block([],
      zval : colnew_appsln([x], 4, fspace, ispace)[1],
      u : float(exact(x)),
      err : map(lambda([a,b], max(a,b)), err, abs(u-zval)),
      x : x + 0.01),
  print("The exact errors are:"),
  printf(true, "   ~{ ~11,4e~}~%", err));
The exact errors are: 
     1.7389E-10   6.2679E-9   2.1843E-7   9.5743E-6
(%o23)                        false

48.3.2 Example 2: Deformation of a spherical cap

These equations describe the small finite deformation of a thin shallow spherical cap of constant thickness subject to a quadratically varying axisymmetric external pressure distribution superimposed on a uniform internal pressure distribution. The problem is described in Parker&Wan 1984 and is Example 2 from Ascher 1981a. The maxima code is in file share/colnew/prob2.mac and a Fortran implementation is in share/colnew/ex2.

There are two nonlinear differential equations for φ and ψ over 0 < x < 1.

(ε^4/μ)[φ'' + (1/x) φ' - (1/x^2) φ] + ψ (1-φ/x) - φ = - γ x (1-(1/2)x^2)

μ [ψ'' + (1/x) ψ' - (1/x^2)ψ] - φ(1-φ/(2x)) = 0

subject to boundary conditions φ = 0 and x ψ' - 0.3 ψ + 0.7 x = 0 at x=0 and x=1.

For ε = μ = 0.01, two solutions exists. These are obtained by starting the nonlinear iteration from two different guesses to the solution: initially with the default initial guess; and secondly, with the initial conditions given by the function solutn.

There are nconc = 2 differential equations of second order. The list of orders m = [2,2] and mstar = sum(m[i]) = 4.

The vector of unknowns of length mstar=4 is z(x) = [ φ(x), φ'(x), ψ(x), ψ'(x)].

The differential equation is expressed as

[φ''(x), ψ''(x)]

=F(x,z_1,z_2,z_3,z_4)

=[z_1/x^2 - z_2/x + (z_1-z_3 (1-z_1/x) - γ x (1-x^2/2))/(ε^4/μ), z_3/x^2 - z_4/x + z_1 (1-z_1/(2x))/μ]

There are four boundary conditions given by list zeta and function G(z_1,z_2,z_3,z_4).

j	zeta[j]	Condition	g[j]
1	0.0	φ = 0	z_1
2	0.0	x ψ' - 0.3 ψ + 0.7 x = 0	z_3
3	1.0	φ = 0	z_1
4	1.0	x ψ' - 0.3 ψ + 0.7 x = 0	z_4 - 0.3 z_3 + 0.7

giving zeta=[0.0,0.0,1.0,1.0] and G(z_1,z_2,z_3,z_4)=[z_1, z_3, z_1, z_4-0.3*z_3+0.7]

Note that x is not an argument of function G. The value of x=zeta[j] must be substituted.

(%i1) load("colnew")$

(%i2) /* Define constants */
 gamma : 1.1;
(%o2)                          1.1

(%i3) eps : 0.01;
(%o3)                         0.01

(%i4) dmu : eps;
(%o4)                         0.01

(%i5) eps4mu : eps^4/dmu;
(%o5)                        1.0e-6

(%i6) xt : sqrt(2*(gamma-1)/gamma);
(%o6)                  0.42640143271122105

(%i7) /* Number of differential equations */
 ncomp : 2;
(%o7)                           2

(%i8) /* Orders */
 m : [2, 2];

(%o8)                        [2, 2]

(%i9) /* Interval ends */
 aleft : 0.0;
(%o9)                          0.0

(%i10) aright : 1.0;

(%o10)                         1.0

(%i11) /* Locations of side conditions */
 zeta : float([0, 0, 1, 1])$

(%i12) /* Set up parameter array.  */
 ipar : makelist(0,k,1,11);
(%o12)          [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

(%i13) /* Non-linear prob */
 ipar[1] : 1;
(%o13)                          1

(%i14) /* 4 collocation points per subinterval */
 ipar[2] : 4;
(%o14)                          4

(%i15) /* Initial uniform mesh of 10 subintervals */
 ipar[3] : 10;
(%o15)                         10

(%i16) ipar[8] : 0;
(%o16)                          0

(%i17) /* Size of fspace, ispace */
 ipar[5] : 40000;
(%o17)                        40000

(%i18) ipar[6] : 2500;
(%o18)                        2500

(%i19) /* No output */
 ipar[7] : 1;
(%o19)                          1

(%i20) /* No initial approx is provided */
 ipar[9] : 0;
(%o20)                          0

(%i21) /* Regular problem */
 ipar[10] : 0;
(%o21)                          0

(%i22) /* No fixed points in mesh */
 ipar[11] : 0;
(%o22)                          0

(%i23) /* Tolerances on all components */
 ipar[4] : 4;

(%o23)                          4

(%i24) /* Tolerances on all four components */
 ltol : [1, 2, 3, 4];
(%o24)                    [1, 2, 3, 4]

(%i25) tol : [1d-5, 1d-5, 1d-5, 1d-5];

(%o25)          [1.0e-5, 1.0e-5, 1.0e-5, 1.0e-5]

(%i26) fspace : makelist(0d0, k, 1, ipar[5])$
(%i27) ispace : makelist(0, k, 1, ipar[6])$

(%i28) fixpnt : []$

(%i29) /* Define the equations */
 fsub(x, z1, z2, z3, z4) :=
 [z1/x/x - z2/x + (z1-z3*(1-z1/x) - gamma*x*(1-x*x/2))/eps4mu,
  z3/x/x - z4/x + z1*(1-z1/2/x)/dmu];

(%o29) fsub(x, z1, z2, z3, z4) := 
 z1                     z1                     x x
 --        z1 - z3 (1 - --) + (- gamma) x (1 - ---)
 x    z2                x                       2
[-- - -- + ----------------------------------------, 
 x    x                     eps4mu
                  z1
                  --
z3                2
--        z1 (1 - --)
x    z4           x
-- - -- + -----------]
x    x        dmu

(%i30) df : jacobian(fsub(x,z1, z2, z3, z4),[z1,z2,z3,z4]);
(%o30) 
      [             z3        1      1             z1           ]
      [  1000000.0 (-- + 1) + --   - -  1000000.0 (-- - 1)   0  ]
      [             x          2     x             x            ]
      [                       x                                 ]
      [                                                         ]
      [            z1     50.0 z1               1             1 ]
      [ 100.0 (1 - ---) - -------   0           --          - - ]
      [            2 x       x                   2            x ]
      [                                         x               ]

(%i31) dfsub(x, z1, z2, z3, z4) :=
  subst(['x=x,'z1=z1,'z2=z2,'z3=z3,'z4=z4], df);

(%o31) dfsub(x, z1, z2, z3, z4) := 
      subst(['x = x, 'z1 = z1, 'z2 = z2, 'z3 = z3, 'z4 = z4], df)

(%i32) g(z1, z2, z3, z4) := [z1, z3, z1, z4 - 0.3*z3 + .7];
(%o32) g(z1, z2, z3, z4) := [z1, z3, z1, z4 - 0.3 z3 + 0.7]

(%i33) gsub(i, z1, z2, z3, z4) :=
    subst(['z1=z1,'z2=z2,'z3=z3,'z4=z4], g(z1, z2, z3, z4)[i]);

(%o33) gsub(i, z1, z2, z3, z4) := 
subst(['z1 = z1, 'z2 = z2, 'z3 = z3, 'z4 = z4], 
g(z1, z2, z3, z4) )
                 i

(%i34) dg:jacobian(g(z1, z2, z3, z4), [z1,z2,z3,z4]);
                       [ 1  0    0    0 ]
                       [                ]
                       [ 0  0    1    0 ]
(%o34)                 [                ]
                       [ 1  0    0    0 ]
                       [                ]
                       [ 0  0  - 0.3  1 ]

(%i35) dgsub(i, z1, z2, z3, z4) := subst(['z1=z1,'z2=z2,'z3=z3,'z4=z4], row(dg, i)[1]);

(%o35) dgsub(i, z1, z2, z3, z4) := 
     subst(['z1 = z1, 'z2 = z2, 'z3 = z3, 'z4 = z4], row(dg, i) )
                                                               1

(%i36) /* Initial approximation function for second run */
 solutn(x) :=
 block([cons : gamma*x*(1-0.5*x*x),
       dcons : gamma*(1-1.5*x*x),
       d2cons : -3*gamma*x],
  if is(x > xt) then
    [[0, 0, -cons, -dcons],
     [0, -d2cons]]
  else
    [[2*x, 2, -2*x + cons, -2 + dcons],
     [0, d2cons]]);

(%o36) solutn(x) := block([cons : gamma x (1 - 0.5 x x), 
dcons : gamma (1 - 1.5 x x), d2cons : - 3 gamma x], 
if is(x > xt) then [[0, 0, - cons, - dcons], [0, - d2cons]]
 else [[2 x, 2, - 2 x + cons, - 2 + dcons], [0, d2cons]])

(%i37) /* First run with default initial guess */
 [iflag, fspace, ispace] :
 colnew_expert(ncomp, m, aleft, aright, zeta, ipar, ltol, tol, fixpnt, ispace, fspace,
 0, fsub, dfsub, gsub, dgsub, dummy)$

(%i38) /* Check return status iflag, 1 = success */
 iflag;

(%o38)                          1

(%i39) /* Print values of solution at x = 0,.05,...,1 */
 x : 0;
(%o39)                          0

(%i40) for j : 1 thru 21 do
 block([],
   zval : colnew_appsln([x], 4, fspace, ispace)[1],
   printf(true, "~5,2f  ~{~15,5e~}~%", x, zval),
   x : x + 0.05);

 0.00       0.00000E+0     4.73042E-2   -3.39927E-32    -1.10497E+0
 0.05       2.36520E-3     4.73037E-2    -5.51761E-2    -1.10064E+0
 0.10       4.73037E-3     4.73030E-2    -1.09919E-1    -1.08765E+0
 0.15       7.09551E-3     4.73030E-2    -1.63796E-1    -1.06600E+0
 0.20       9.46069E-3     4.73039E-2    -2.16375E-1    -1.03569E+0
 0.25       1.18259E-2     4.73040E-2    -2.67221E-1    -9.96720E-1
 0.30       1.41911E-2     4.73020E-2    -3.15902E-1    -9.49092E-1
 0.35       1.65562E-2     4.72980E-2    -3.61986E-1    -8.92804E-1
 0.40       1.89215E-2     4.72993E-2    -4.05038E-1    -8.27857E-1
 0.45       2.12850E-2     4.72138E-2    -4.44627E-1    -7.54252E-1
 0.50       2.36370E-2     4.67629E-2    -4.80320E-1    -6.72014E-1
 0.55       2.59431E-2     4.51902E-2    -5.11686E-1    -5.81260E-1
 0.60       2.81093E-2     4.07535E-2    -5.38310E-1    -4.82374E-1
 0.65       2.99126E-2     2.98538E-2    -5.59805E-1    -3.76416E-1
 0.70       3.08743E-2     5.53985E-3    -5.75875E-1    -2.65952E-1
 0.75       3.00326E-2    -4.51680E-2    -5.86417E-1    -1.56670E-1
 0.80       2.55239E-2    -1.46617E-1    -5.91753E-1    -6.04539E-2
 0.85       1.37512E-2    -3.46952E-1    -5.93069E-1    -1.40102E-3
 0.90      -1.25155E-2    -7.52826E-1    -5.93303E-1    -2.86234E-2
 0.95      -6.94274E-2    -1.65084E+0    -5.99062E-1    -2.48115E-1
 1.00      2.64233E-14     1.19263E+2    -6.25420E-1    -8.87626E-1
(%o40)                        done

(%i41) /* Second run with initial guess */
 ipar[9] : 1;
(%o41)                          1

(%i42) [iflag, fspace, ispace] :
 colnew_expert(ncomp, m, aleft, aright, zeta, ipar, ltol, tol, fixpnt, ispace, fspace,
 0, fsub, dfsub, gsub, dgsub, solutn)$

(%i43) /* Check return status iflag, 1 = success */
 iflag;

(%o43)                          1

(%i44) /* Print values of solution at x = 0,.05,...,1 */
 x : 0;
(%o44)                          0

(%i45) for j : 1 thru 21 do
 block([],
   zval : colnew_appsln([x], 4, fspace, ispace)[1],
   printf(true, "~5,2f  ~{~15,5e~}~%", x, zval),
   x : x + 0.05);
 0.00       0.00000E+0     2.04139E+0     0.00000E+0    -9.03975E-1
 0.05       1.02070E-1     2.04139E+0    -4.52648E-2    -9.07936E-1
 0.10       2.04139E-1     2.04139E+0    -9.09256E-2    -9.19819E-1
 0.15       3.06209E-1     2.04140E+0    -1.37379E-1    -9.39624E-1
 0.20       4.08279E-1     2.04141E+0    -1.85020E-1    -9.67352E-1
 0.25       5.10351E-1     2.04152E+0    -2.34246E-1    -1.00301E+0
 0.30       6.12448E-1     2.04303E+0    -2.85454E-1    -1.04663E+0
 0.35       7.15276E-1     2.10661E+0    -3.39053E-1    -1.09916E+0
 0.40       8.32131E-1    -2.45181E-1    -3.96124E-1    -1.20544E+0
 0.45       1.77510E-2    -3.57554E+0    -4.45400E-1    -7.13543E-1
 0.50       2.25122E-2     1.23608E-1    -4.80360E-1    -6.70074E-1
 0.55       2.58693E-2     4.85257E-2    -5.11692E-1    -5.81075E-1
 0.60       2.80994E-2     4.11112E-2    -5.38311E-1    -4.82343E-1
 0.65       2.99107E-2     2.99116E-2    -5.59805E-1    -3.76409E-1
 0.70       3.08739E-2     5.55200E-3    -5.75875E-1    -2.65950E-1
 0.75       3.00325E-2    -4.51649E-2    -5.86417E-1    -1.56669E-1
 0.80       2.55239E-2    -1.46616E-1    -5.91753E-1    -6.04538E-2
 0.85       1.37512E-2    -3.46952E-1    -5.93069E-1    -1.40094E-3
 0.90      -1.25155E-2    -7.52826E-1    -5.93303E-1    -2.86233E-2
 0.95      -6.94274E-2    -1.65084E+0    -5.99062E-1    -2.48115E-1
 1.00      2.65413E-14     1.19263E+2    -6.25420E-1    -8.87626E-1
(%o45)                        done

Columns 1 (x) and 2 (φ) of the two sets of results above, and the figure below, can be compared with Figure 1 in Ascher 1981a.

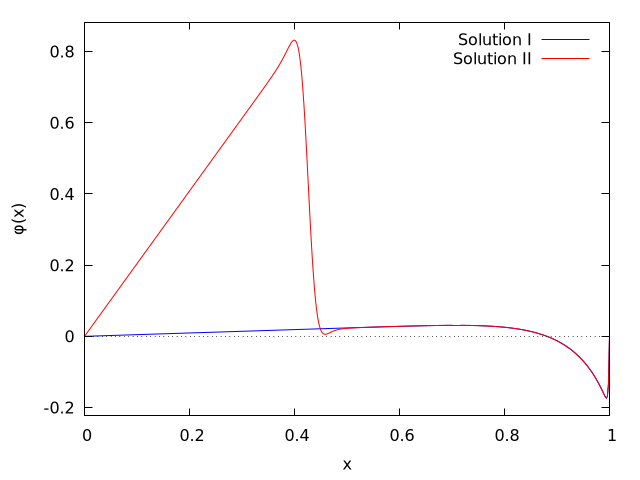
48.3.3 Example 3: Rotating flow of viscous incompressible fluid

Example 3 from Ascher 1981a describes the velocities in the boundary layer produced by the rotating flow of a viscous incompressible fluid over a stationary infinite disk (see Gawain&Ball 1978).

The solution uses a number of techniques to obtain convergence. Refer to Ascher 1981a for details.

The code is in directory share/colnew. The maxima code is in file prob3.mac. The reference Fortran implementation is in directory ex3.

48.3.4 Example 4: Quantum Neumann equation

A more sophisticated example is Bellon&Talon 2005, which deals with singularities in the solution domain, provides an initial quess to the solution and uses continuation to solve the system of non-linear differential equations.

The code is in directory share/colnew. The maxima code is in file prob4.mac. The Fortran implementation is in directory ex4.

48.3.5 Example 5: Simple example of continuation

This example (see Ascher et al, 1995, Example 9.2) solves a numerically difficult boundary value problem using continuation.

The linear differential equation is

ε u'' + x u' = -ε π^2 cos(πx) - (πx) sin(πx), -1 < x < 1

with boundary conditions

u(-1)=-2 and u(1)=0

The exact solution is

u(x) = cos(πx) + erf(x/sqrt(2ε))/erf(1/sqrt(2ε))

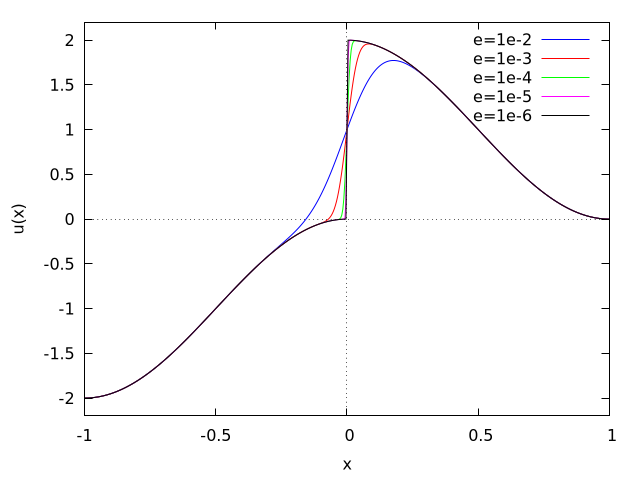
When ε is small the solution has a rapid transition near x=0 and is difficult to solve numerically. COLNEW is able to solve the problem for directly for ε=1.0e-6, but here we will use continuation to solve it succesively for ε=[1e-2,1e-3,1e-4,1e-5,1e-6].

There is nconc = 1 differential equation of second order. The list of orders m = [2] and mstar = sum(m[j]) = 2.

The unknown vector of length mstar is z(x) = [z_1(x),z_2(x)] = [u(x),u'(x)].

The differential equation is expressed as [u''(x)] = F(x,z_1,z_2) = [-(x/ε)z_2 - π^2cos(πx) - (πx/ε)sin(πx)]

There are mstar=2 boundary conditions. They are given by a function G(z_1,z_2) that returns a list of length mstar. The j-th boundary condition applies at x = zeta[j] and is satisfied when g[j] = 0. We have

j	zeta[j]	Condition	g[j]
1	-1.0	u=-2	z_1+2
2	1.0	u=0	z_1

giving zeta = [-1.0,1,0] and G(z_1,z_2) = [z_1+2, z_1].

The Jacobians df and dg of f and g respectively are determined symbolically.

The ODE will be solved for multiple values of ε. The functions fsub, dfsub, gsub and dgsub are defined before e is set, so that it can be changed in the program.

(%i1) load("colnew")$
(%i2) kill(e,x,z1,z2)$

(%i3) /* Exact solution */
 exact(x):=cos(%pi*x)+erf(x/sqrt(2*e))/erf(1/sqrt(2*e))$

(%i4) /* Define the equations.  Do this before e is defined */
 f: [-(x/e)*z2 - %pi^2*cos(%pi*x) - (%pi*x/e)*sin(%pi*x)];
             x z2   %pi x sin(%pi x)      2
(%o4)     [- ---- - ---------------- - %pi  cos(%pi x)]
              e            e

(%i5) define(fsub(x,z1,z2),f);
                            x z2   %pi x sin(%pi x)
(%o5) fsub(x, z1, z2) := [- ---- - ----------------
                             e            e
                                                    2
                                               - %pi  cos(%pi x)]

(%i6) df: jacobian(f,[z1,z2]);
                           [      x ]
(%o6)                      [ 0  - - ]
                           [      e ]

(%i7) define(dfsub(x,z1,z2),df);
                                     [      x ]
(%o7)            dfsub(x, z1, z2) := [ 0  - - ]
                                     [      e ]

(%i8) /* Build the functions gsub and dgsub
   Use define and buildq to remove dependence on g and dg */
 g: [z1+2,z1];
(%o8)                     [z1 + 2, z1]

(%i9) define(gsub(i,z1,z2),buildq([g],g[i]));
(%o9)           gsub(i, z1, z2) := [z1 + 2, z1]
                                               i

(%i10) dg: jacobian(g,[z1,z2]);
                            [ 1  0 ]
(%o10)                      [      ]
                            [ 1  0 ]

(%i11) define(
 dgsub(i,z1,z2),
 buildq([val:makelist(dg[i],i,1,length(dg))],block([dg:val],dg[i])));
(%o11) dgsub(i, z1, z2) := block([dg : [[1, 0], [1, 0]]], dg )
                                                            i

(%i12) /* Define constant epsilon */
 e : 0.01$

(%i13) /* Number of differential equations */
 ncomp : 1$

(%i14) /* Orders */
 m : [2]$

(%i15) /* Interval ends */
 aleft:-1.0$

(%i16) aright:1.0$

(%i17) /* Locations of side conditions */
 zeta : float([-1, 1])$

(%i18) /* Set up parameter array.  */
 ipar : makelist(0,k,1,11)$

(%i19) /* linear prob */
 ipar[1] : 0$

(%i20) /* 5 collocation points per subinterval */
 ipar[2] : 5$

(%i21) /* Initial uniform mesh of 1 subintervals */
 ipar[3] : 1$

(%i22) ipar[8] : 0$

(%i23) /* Size of fspace, ispace */
 ipar[5] : 10000$

(%i24) ipar[6] :  1000$

(%i25) /* No output.  Don't do this for development. */
 ipar[7]:1$

(%i26) /* No initial guess is provided */
 ipar[9] : 0$

(%i27) /* Regular problem */
 ipar[10] : 0$

(%i28) /* No fixed points in mesh */
 ipar[11] : 0$

(%i29) /* Tolerances on two components */
 ipar[4] : 2$

(%i30) /* Two error tolerances (on u and its derivative)
   Relatively large tolerances to keep the example small */
 ltol : [1, 2]$

(%i31) tol : [1e-4, 1e-4]$
(%i32) fspace : makelist(0e0, k, 1, ipar[5])$
(%i33) ispace : makelist(0, k, 1, ipar[6])$
(%i34) fixpnt : []$

(%i35) /* First run with default initial guess.
   Returns iflag. 1 = success */
 ([iflag, fspace, ispace] :
  colnew_expert(ncomp, m, aleft, aright, zeta, ipar, ltol, tol,
  fixpnt, ispace, fspace,
  0, fsub, dfsub, gsub, dgsub, dummy),
  if (iflag#1) then error("On return from colnew_expert: iflag = ",iflag),
  iflag);
(%o35)                          1

(%i36) /* Function to generate equally spaced list of values */
 xlist(xmin,xmax,n):=block([dx:(xmax-xmin)/n],makelist(i,i,0,n)*dx+xmin)$

(%i37) /* x values for solution.  Cluster around x=0 */
 X: xlist(aleft,aright,500)$

(%i38) /* Generate solution values for z1=u(x) */
 ans:colnew_appsln(X,2,fspace,ispace)$

(%i39) z:maplist(first,ans)$
(%i40) Z:[z]$

(%i41) /* Compare with exact solution and report */
 y:float(map(exact,X))$

(%i42) maxerror:apply(max,abs(y-z));
(%o42)                6.881499912125832e-7

(%i43) printf(true," e: ~8,3e  iflag ~3d  Mesh size ~3d  max error ~8,3e~%",
  e,iflag,ispace[1],maxerror);
 e: 1.000E-2  iflag   1  Mesh size  16  max error 6.881E-7
(%o43)                        false

(%i44) /* Now use continuation to solve for progressively smaller e
   Use previous solution as initial guess and every second point
   from previous mesh as initial mesh */
 ipar[9] : 3$

(%i45) /* Run COLNEW using continuation for new value of e
   Set new mesh size ipar[3] from previous size ispace[1]
   Push list of values of z1=u(x) on to list Z */
 run_it(e_):=block(
  e:e_,
  ipar[3]:ispace[1],
  [iflag, fspace, ispace]:
     colnew_expert(ncomp,m,aleft,aright,zeta,ipar,ltol,tol,fixpnt,
     ispace,fspace,0,fsub,dfsub,gsub,dgsub,dummy),
  if (iflag#1) then error("On return from colnew_expert: iflag =",iflag),
  ans:colnew_appsln(X,2,fspace,ispace),
  z:maplist(first,ans),
  push(z,Z),
  y:float(map(exact,X)),
  maxerror:apply(max,abs(y-z)),
  printf(true," e: ~8,3e  iflag ~3d  Mesh size ~3d  max error ~8,3e~%",
    e,iflag,ispace[1],maxerror),
  iflag
 )$

(%i46) for e_ in [1e-3,1e-4,1e-5,1e-6] do run_it(e_)$
 e: 1.000E-3  iflag   1  Mesh size  20  max error 3.217E-7
 e: 1.000E-4  iflag   1  Mesh size  40  max error 3.835E-7
 e: 1.000E-5  iflag   1  Mesh size  38  max error 8.690E-9
 e: 1.000E-6  iflag   1  Mesh size  60  max error 6.313E-7

(%i47) /* Z is list of solutions z1 = u(x).  Restore order. */
 Z:reverse(Z)$

(%i48) /* Plot z1=u(x) for each value of e
 plot2d([
  [discrete,X,Z[1]], [discrete,X,Z[2]], [discrete,X,Z[3]],
  [discrete,X,Z[4]], [discrete,X,Z[5]]],
  [legend,"e=1e-2","e=1e-3","e=1e-4","e=1e-5","e=1e-6"],
  [xlabel,"x"],[ylabel,"u(x)"],
  [png_file,"./colnew-ex5.png"]); */
 done$

The figure below shows the solution for ε=[10^{-2},10^{-3},10^{-4},10^{-5},10^{-6}].

48.4 References for colnew

(Gawain&Ball 1978) T. H. Gawain and R. E. Ball, Improved Finite Difference Formulas for Boundary Value Problems, International Journal for Numerical Methods in Engineering 12, no. 7 (1978) 1151–60. doi:10.1002/nme.1620120706
(Ascher 1979a) U. Ascher, J. Christiansen and R. D. Russell, A collocation solver for mixed order systems of boundary value problems, Math. Comp. 33 (1979), 659-679, doi:10.1090/S0025-5718-1979-0521281-7
(Ascher 1979b) U. Ascher, J. Christiansen and R. D. Russell, COLSYS - a collocation code for boundary value problems, in Codes for boundary-value problems in ordinary differential equations, Lecture Notes in Computer Science 76, Springer Verlag, B. Childs et. al. (eds.) (1979), 164-185, ISBN 978-3-540-09554-5
(Ascher 1981a) U. Ascher, J. Christiansen and R. D. Russell, Collocation software for boundary-value odes, ACM Trans. Math Software 7 (1981), 209-222. doi:10.1145/355945.355950
(Ascher 1981b) U. Ascher, U., J. Christiansen, and R. D. Russell. ‘Algorithm 569: COLSYS: Collocation Software for Boundary-Value ODEs [D2]’. ACM Transactions on Mathematical Software 7, no. 2 (June 1981): 223–29. doi:10.1145/355945.355951
(Ascher&Russell 1981) U. Ascher and R. D. Russell. ‘Reformulation of Boundary Value Problems into “Standard” Form’. SIAM Review 23, no. 2 (April 1981), 238–54, doi:10.1137/1023039
(Parker&Wan 1984) David F. Parker and Frederic Y. M. Wan, ‘Finite Polar Dimpling of Shallow Caps Under Sub-Buckling Axisymmetric Pressure Distributions’. SIAM Journal on Applied Mathematics 44, no. 2 (April 1984): 301–26, doi:10.1137/0144022
(Bader&Ascher 1987) G. Bader and U. Ascher, A new basis implementation for a mixed order boundary value ode solver, SIAM J. Scient. Stat. Comput. (1987), 483-500, doi:10.1137/0908047
(Ascher et al, 1995) Uri M. Ascher, Robert M. M. Mattheij, and Robert D. Russell. Numerical Solution of Boundary Value Problems for Ordinary Differential Equations. Classics in Applied Mathematics 13, SIAM, (1995), ISBN 978-0-89871-354-1
(Bellon&Talon 2005) M. Bellon, M. Talon, Spectrum of the quantum Neumann model, Physics Letters A, Volume 337, Issues 4–6, pp 360-368, doi:10.1016/j.physleta.2005.02.002 arXiv:hep-th/0407005