16 Elliptic Functions ¶
- Introduction to Elliptic Functions and Integrals
- Functions and Variables for Elliptic Functions
- Functions and Variables for Elliptic Integrals
16.1 Introduction to Elliptic Functions and Integrals ¶
Maxima includes support for Jacobian elliptic functions and for complete and incomplete elliptic integrals. This includes symbolic manipulation of these functions and numerical evaluation as well. Definitions of these functions and many of their properties can by found in Abramowitz and Stegun, A&S Chapter 16 and A&S Chapter 17. See also DLMF 22.2. As much as possible, we use the definitions and relationships given in Abramowitz and Stegun.
In particular, all elliptic functions and integrals use the parameter \(m\) instead of the modulus \(k\) or the modular angle \(\alpha\). The following relationships are true:
\[\eqalign{
m &= k^2 \cr
k &= \sin\alpha
}
\]
Note that Abramowitz and Stegun uses the notation \({\rm sn}(u|m)\) where we use \({\rm sn}(u,m)\) instead. The DLMF uses modulus \(k\) instead of the parameter \(m\).
The elliptic functions and integrals are primarily intended to support symbolic computation. Therefore, most of derivatives of the functions and integrals are known. However, if floating-point values are given, a floating-point result is returned.
Support for most of the other properties of elliptic functions and integrals other than derivatives has not yet been written.
Some examples of elliptic functions:
(%i1) jacobi_sn (u, m); (%o1) jacobi_sn(u, m)
(%i2) jacobi_sn (u, 1); (%o2) tanh(u)
(%i3) jacobi_sn (u, 0); (%o3) sin(u)
(%i4) diff (jacobi_sn (u, m), u); (%o4) jacobi_cn(u, m) jacobi_dn(u, m)
(%i5) diff (jacobi_sn (u, m), m);
(%o5) (jacobi_cn(u, m) jacobi_dn(u, m)
elliptic_e(asin(jacobi_sn(u, m)), m)
(u - ------------------------------------))/(2 m)
1 - m
2
jacobi_cn (u, m) jacobi_sn(u, m)
+ --------------------------------
2 (1 - m)
Some examples of elliptic integrals:
(%i1) elliptic_f (phi, m); (%o1) elliptic_f(phi, m)
(%i2) elliptic_f (phi, 0); (%o2) phi
(%i3) elliptic_f (phi, 1);
phi %pi
(%o3) log(tan(--- + ---))
2 4
(%i4) elliptic_e (phi, 1);
phi phi
(%o4) 2 round(---) - sin(%pi round(---) - phi)
%pi %pi
(%i5) elliptic_e (phi, 0); (%o5) phi
(%i6) elliptic_kc (1/2);
3/2
%pi
(%o6) -----------
2 3
2 gamma (-)
4
(%i7) makegamma (%);
3/2
%pi
(%o7) -----------
2 3
2 gamma (-)
4
(%i8) diff (elliptic_f (phi, m), phi);
1
(%o8) ---------------------
2
sqrt(1 - m sin (phi))
(%i9) diff (elliptic_f (phi, m), m);
elliptic_e(phi, m) - (1 - m) elliptic_f(phi, m)
(%o9) (-----------------------------------------------
m
cos(phi) sin(phi)
- ---------------------)/(2 (1 - m))
2
sqrt(1 - m sin (phi))
Support for elliptic functions and integrals was written by Raymond Toy. It is placed under the terms of the General Public License (GPL) that governs the distribution of Maxima.
16.2 Functions and Variables for Elliptic Functions ¶
See A&S Section 6.12 and DLMF 22.2 for more information.
- Function: jacobi_sn (u, m) ¶
The Jacobian elliptic function \({\rm sn}(u,m).\)
Categories: Elliptic functions ·
- Function: jacobi_cn (u, m) ¶
The Jacobian elliptic function \({\rm cn}(u,m).\)
Categories: Elliptic functions ·
- Function: jacobi_dn (u, m) ¶
The Jacobian elliptic function \({\rm dn}(u,m).\)
Categories: Elliptic functions ·
- Function: jacobi_ns (u, m) ¶
The Jacobian elliptic function \({\rm ns}(u,m) = 1/{\rm sn}(u,m).\)
Categories: Elliptic functions ·
- Function: jacobi_sc (u, m) ¶
The Jacobian elliptic function \({\rm sc}(u,m) = {\rm sn}(u,m)/{\rm cn}(u,m).\)
Categories: Elliptic functions ·
- Function: jacobi_sd (u, m) ¶
The Jacobian elliptic function \({\rm sd}(u,m) = {\rm sn}(u,m)/{\rm dn}(u,m).\)
Categories: Elliptic functions ·
- Function: jacobi_nc (u, m) ¶
The Jacobian elliptic function \({\rm nc}(u,m) = 1/{\rm cn}(u,m).\)
Categories: Elliptic functions ·
- Function: jacobi_cs (u, m) ¶
The Jacobian elliptic function \({\rm cs}(u,m) = {\rm cn}(u,m)/{\rm sn}(u,m).\)
Categories: Elliptic functions ·
- Function: jacobi_cd (u, m) ¶
The Jacobian elliptic function \({\rm cd}(u,m) = {\rm cn}(u,m)/{\rm dn}(u,m).\)
Categories: Elliptic functions ·
- Function: jacobi_nd (u, m) ¶
The Jacobian elliptic function \({\rm nd}(u,m) = 1/{\rm dn}(u,m).\)
Categories: Elliptic functions ·
- Function: jacobi_ds (u, m) ¶
The Jacobian elliptic function \({\rm ds}(u,m) = {\rm dn}(u,m)/{\rm sn}(u,m).\)
Categories: Elliptic functions ·
- Function: jacobi_dc (u, m) ¶
The Jacobian elliptic function \({\rm dc}(u,m) = {\rm dn}(u,m)/{\rm cn}(u,m).\)
Categories: Elliptic functions ·
- Function: jacobi_am (u, m) ¶
The Jacobi amplitude function,
jacobi_am, is defined implicitly by (see http://functions.wolfram.com/09.24.02.0001.01) \(z = {\rm am}(w, m)\) where \(w = F(z,m)\) where \(F(z,m)\) is the incomplete elliptic integral of the first kind (see elliptic_f). It is defined for all real and complex values of \(z\) and \(m\). In particular for real \(z\) and \(m\) with \(|m|<1\), \({\rm am}(z,m)\) maps the entire real line to the entire real line. For other values of \(z\) and \(m\), the following relationship is used: \({\rm am}(z,m) = \sin^{-1}({\rm jacobi\_sn}(z, m)).\)Some examples:
(%i1) jacobi_am(z,0); (%o1) z
(%i2) jacobi_am(z,1); z %pi (%o2) 2 atan(%e ) - --- 2(%i3) jacobi_am(0,m); (%o3) 0
(%i4) jacobi_am(100, .5); (%o4) 84.70311272411382
(%i5) jacobi_am(0.5, 1.5); (%o5) 0.4707197897046991
(%i6) jacobi_am(1.5b0, 1.5b0+%i); (%o6) 9.340542168700782b-1 - 3.723960452146071b-1 %i
(%i1) plot2d([jacobi_am(x,.4),jacobi_am(x,.7),jacobi_am(x,.99),jacobi_am(x,.999999)],[x,0,10*%pi]); (%o1) false
Compare this plot with the plot from DLMF 22.16.iv:
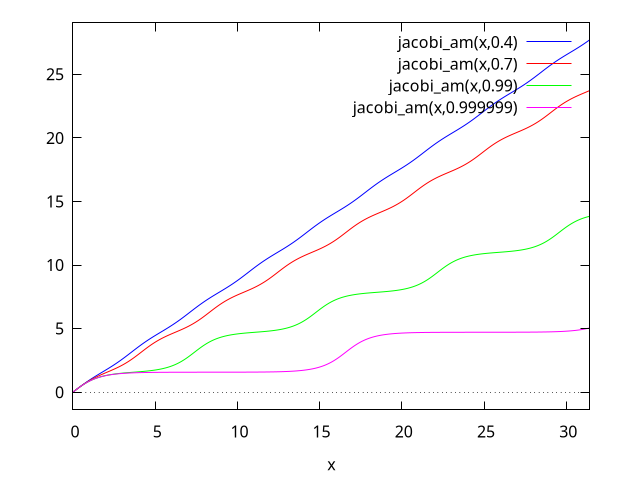Categories: Elliptic functions ·
- Function: inverse_jacobi_dn (u, m) ¶
The inverse of the Jacobian elliptic function \({\rm dn}(u,m).\) For \(\sqrt{1-m}\le u \le 1,\) it can also be written (DLMF 22.15.E14):
\[{\rm inverse\_jacobi\_dn}(u, m) = \int_u^1 {dt\over \sqrt{(1-t^2)(t^2-(1-m))}} \]Categories: Elliptic functions ·
- Function: inverse_jacobi_ns (u, m) ¶
The inverse of the Jacobian elliptic function \({\rm ns}(u,m).\) For \(1 \le u,\) it can also be written (DLMF 22.15.E121):
\[{\rm inverse\_jacobi\_ns}(u, m) = \int_u^{\infty} {dt\over \sqrt{(1-t^2)(t^2-m)}} \]Categories: Elliptic functions ·
- Function: inverse_jacobi_sc (u, m) ¶
The inverse of the Jacobian elliptic function \({\rm sc}(u,m).\) For all \(u\) it can also be written (DLMF 22.15.E20):
\[{\rm inverse\_jacobi\_sc}(u, m) = \int_0^u {dt\over \sqrt{(1+t^2)(1+(1-m)t^2)}} \]Categories: Elliptic functions ·
- Function: inverse_jacobi_sd (u, m) ¶
The inverse of the Jacobian elliptic function \({\rm sd}(u,m).\) For \(-1/\sqrt{1-m}\le u \le 1/\sqrt{1-m},\) it can also be written (DLMF 22.15.E16):
\[{\rm inverse\_jacobi\_sd}(u, m) = \int_0^u {dt\over \sqrt{(1-(1-m)t^2)(1+mt^2)}} \]Categories: Elliptic functions ·
- Function: inverse_jacobi_nc (u, m) ¶
The inverse of the Jacobian elliptic function \({\rm nc}(u,m).\) For \(1\le u,\) it can also be written (DLMF 22.15.E19):
\[{\rm inverse\_jacobi\_nc}(u, m) = \int_1^u {dt\over \sqrt{(t^2-1)(m+(1-m)t^2)}} \]Categories: Elliptic functions ·
- Function: inverse_jacobi_cs (u, m) ¶
The inverse of the Jacobian elliptic function \({\rm cs}(u,m).\) For all \(u\) it can also be written (DLMF 22.15.E23):
\[{\rm inverse\_jacobi\_cs}(u, m) = \int_u^{\infty} {dt\over \sqrt{(1+t^2)(t^2+(1-m))}} \]Categories: Elliptic functions ·
- Function: inverse_jacobi_cd (u, m) ¶
The inverse of the Jacobian elliptic function \({\rm cd}(u,m).\) For \(-1\le u \le 1,\) it can also be written (DLMF 22.15.E15):
\[{\rm inverse\_jacobi\_cd}(u, m) = \int_u^1 {dt\over \sqrt{(1-t^2)(1-mt^2)}} \]Categories: Elliptic functions ·
- Function: inverse_jacobi_nd (u, m) ¶
The inverse of the Jacobian elliptic function \({\rm nd}(u,m).\) For \(1\le u \le 1/\sqrt{1-m},\) it can also be written (DLMF 22.15.E17):
\[{\rm inverse\_jacobi\_nd}(u, m) = \int_1^u {dt\over \sqrt{(t^2-1)(1-(1-m)t^2)}} \]Categories: Elliptic functions ·
- Function: inverse_jacobi_ds (u, m) ¶
The inverse of the Jacobian elliptic function \({\rm ds}(u,m).\) For \(\sqrt{1-m}\le u,\) it can also be written (DLMF 22.15.E22):
\[{\rm inverse\_jacobi\_ds}(u, m) = \int_u^{\infty} {dt\over \sqrt{(t^2+m)(t^2-(1-m))}} \]Categories: Elliptic functions ·
- Function: inverse_jacobi_dc (u, m) ¶
The inverse of the Jacobian elliptic function \({\rm dc}(u,m).\) For \(1 \le u,\) it can also be written (DLMF 22.15.E18):
\[{\rm inverse\_jacobi\_dc}(u, m) = \int_1^u {dt\over \sqrt{(t^2-1)(t^2-m)}} \]Categories: Elliptic functions ·
16.3 Functions and Variables for Elliptic Integrals ¶
- Function: elliptic_f (phi, m) ¶
The incomplete elliptic integral of the first kind, defined as
\[\int_0^{\phi} {\frac{d\theta}{\sqrt{1-m\sin^2\theta}}} \]See also elliptic_e and elliptic_kc.
Categories: Elliptic integrals ·
- Function: elliptic_e (phi, m) ¶
The incomplete elliptic integral of the second kind, defined as
\[\int_0^\phi {\sqrt{1 - m\sin^2\theta}}\, d\theta \]See also elliptic_f and elliptic_ec.
Categories: Elliptic integrals ·
- Function: elliptic_eu (u, m) ¶
The incomplete elliptic integral of the second kind, defined as
\[E(u, m) = \int_0^u {\rm dn}(v, m)\, dv = \int_0^\tau \sqrt{\frac{1-m t^2}{1-t^2}}\, dt \]where \(\tau = {\rm sn}(u,m) .\)
This is related to
elliptic_eby\[E(u,m) = E(\sin^{-1} {\rm sn}(u, m), m) \]See also elliptic_e.
Categories: Elliptic integrals ·
- Function: elliptic_pi (n, phi, m) ¶
The incomplete elliptic integral of the third kind, defined as
\[\int_0^\phi {{d\theta}\over{(1-n\sin^2 \theta)\sqrt{1 - m\sin^2\theta}}} \]Categories: Elliptic integrals ·
- Function: elliptic_kc (m) ¶
The complete elliptic integral of the first kind, defined as
\[\int_0^{\frac{\pi}{2}} {{d\theta}\over{\sqrt{1 - m\sin^2\theta}}} \]For certain values of \(m\), the value of the integral is known in terms of \(Gamma\) functions. Use
makegammato evaluate them.Categories: Elliptic integrals ·
- Function: elliptic_ec (m) ¶
The complete elliptic integral of the second kind, defined as
\[\int_0^{\frac{\pi}{2}} \sqrt{1 - m\sin^2\theta}\, d\theta \]For certain values of \(m\), the value of the integral is known in terms of \(Gamma\) functions. Use
makegammato evaluate them.Categories: Elliptic integrals ·
- Function: carlson_rc (x, y) ¶
Carlson’s RC integral is defined by
\[R_C(x, y) = \frac{1}{2} \int_0^{\infty} \frac{1}{\sqrt{t+x}(t+y)}\, dt \]See Numerical Computation of Real or Complex Elliptic Integrals for more information.
This integral is related to many elementary functions in the following way:
\[\eqalign{ \log x &= (x-1) R_C\left(\left({\frac{1+x}{2}}\right)^2, x\right), \quad x > 0 \cr \sin^{-1} x &= x R_C(1-x^2, 1), \quad |x| \le 1 \cr \cos^{-1} x &= \sqrt{1-x^2} R_C(x^2,1), \quad 0 \le x \le 1 \cr \tan^{-1} x &= x R_C(1,1+x^2) \cr \sinh^{-1} x &= x R_C(1+x^2,1) \cr \cosh^{-1} x &= \sqrt{x^2-1} R_C(x^2,1), \quad x \ge 1 \cr \tanh^{-1}(x) &= x R_C(1,1-x^2), \quad |x| \le 1 } \]Also, we have the relationship
\[R_C(x,y) = R_F(x,y,y) \]
Some special values:
\[\eqalign{R_C(0, 1) &= \frac{\pi}{2} \cr R_C(0, 1/4) &= \pi \cr R_C(2,1) &= \log(\sqrt{2} + 1) \cr R_C(i,i+1) &= \frac{\pi}{4} + \frac{i}{2} \log(\sqrt{2}-1) \cr R_C(0,i) &= (1-i)\frac{\pi}{2\sqrt{2}} \cr } \]Categories: Elliptic integrals ·
- Function: carlson_rd (x, y, z) ¶
Carlson’s RD integral is defined by
\[R_D(x,y,z) = \frac{3}{2} \int_0^{\infty} \frac{1}{\sqrt{t+x}\sqrt{t+y}\sqrt{t+z}\,(t+z)}\, dt \]See Numerical Computation of Real or Complex Elliptic Integrals for more information.
We also have the special values
\[\eqalign{ R_D(x,x,x) &= x^{-\frac{3}{2}} \cr R_D(0,y,y) &= \frac{3}{4} \pi y^{-\frac{3}{2}} \cr R_D(0,2,1) &= 3 \sqrt{\pi} \frac{\Gamma(\frac{3}{4})}{\Gamma(\frac{1}{4})} } \]It is also related to the complete elliptic integral of the second kind, \(E\), (
elliptic_ec) as follows\[E(m) = R_F(0, 1 - m, 1) - \frac{m}{3} R_D(0, 1 - m, 1) \]Categories: Elliptic integrals ·
- Function: carlson_rf (x, y, z) ¶
Carlson’s RF integral is defined by
\[R_F(x,y,z) = \frac{1}{2} \int_0^{\infty} \frac{1}{\sqrt{t+x}\sqrt{t+y}\sqrt{t+z}}\, dt \]See Numerical Computation of Real or Complex Elliptic Integrals for more information.
We also have the special values
\[\eqalign{ R_F(0,1,2) &= \frac{\Gamma({\frac{1}{4}})^2}{4\sqrt{2\pi}} \cr R_F(i,-i,0) &= \frac{\Gamma({\frac{1}{4}})^2}{4\sqrt{\pi}} } \]It is also related to the complete elliptic integral of the second kind, \(E\), (
elliptic_ec) as follows\[E(m) = R_F(0, 1 - m, 1) - \frac{m}{3} R_D(0, 1 - m, 1) \]Categories: Elliptic integrals ·
- Function: carlson_rj (x, y, z, p) ¶
Carlson’s RJ integral is defined by
\[R_J(x,y,z) = \frac{1}{2} \int_0^{\infty} \frac{1}{\sqrt{t+x}\sqrt{t+y}\sqrt{t+z}\,(t+p)}\, dt \]See Numerical Computation of Real or Complex Elliptic Integrals for more information.
It is related to the elliptic integral of the third kind (
elliptic_pi) by\[\int_0^\phi {1\over \left(1+n\sin^2\theta\right) \sqrt{1-m\sin^2\theta}} \, d\theta = R_F(c-1,c-m,c) - {n\over 3}R_j(c-1,c-m,c,c+n) \]where \(c = \csc\phi.\) Note that this differs in our definition of
elliptic_piby the sign of the parameter \(n\).Categories: Elliptic integrals ·